| | | |
|---|
| 秋満氏が番組で取り上げる名著の講師を選ぶ大きな基準とされていることは、第一 |
| に、その名著を愛し、深く読み込んでいること、そして、第二に、その名著を深く愛 |
| しながらも、距離をとって客観的な視点で読み解くことができることだそうです。第 |
| 一の場合も、単に愛しているだけでは、その名著への愛情告白だけに終わってしまう |
| おそれがあり、また、第二の距離を持ちすぎてしまうと、ドライな解説に終始して、 |
| 逆にその名著の生き生きとした魅力が伝わらなくなってしまいますので、この微妙な |
| バランスが非常に難しいのだと思われます。カウンセリングの極意は、「温かく突き |
| 放し、冷たく抱き寄せる」ことでしょうが、名著の解説者の資質にも同じことがいえ |
| るのでしょう。 |
| |
| 3.トランプ政権の誕生と世界的な全体主義の復活傾向に |
| タイミングを合わせて取り上げられた「100分de名著」の一冊 |
| 8年前の今月(2017年7月)に自国アメリカ合衆国第一主義、排外主義を掲げてト |
| ランプ政権が誕生しましたが、万全の準備をされていたからでしょう、2ヶ月後の9 |
| 月にはドイツ出身のアメリカ政治哲学者で思想家のドイツ系ユダヤ人ハンナ・アーレ |
| ント(Hannah Arendt)著の“Origins of Totalitarianism 邦訳「全体主義の起源」” |
| が「100分de名著」で取り上げられました。 筆者もGAFAM(ガーファミ、すなわち |
| “Google,Apple,Facebook,Amazonand Microsoft”) やSNSに踊らされて、思考したり |
| 関連した事柄を問い続けることがないがしろにされる現在の世界的な傾向に、何とも |
| 太平洋戦争に入る直前の我が国の軍国政治の世界にも通ずるような一種異様な不気味 |
| さを感じていましたので、この名著は本の焼却を命じたり、人間の思考力を奪う全体 |
| 主義の恐怖が余すところなく描かれているので、現代人にタイミングよく発せられた |
| 鋭い警告と感じたのでした。 |
| 自国アメリカ第一主義(Make America Great Again=MAGA)と排外主義を掲げるト |
| ランプ政権が誕生するやこのアーレントの「名著「全体主義の起源」が全米でベスト |
| セラーになったのです。読者はトランプの進める強権的な政治手法、排外主義的な政 |
| 策に反発した市民たちで、こぞって買い求めたのでした。このタイミングを狙って誕 |
| 生したトランプ政権の後、フランスのルペン、ドイツやオーストリアにおけるネオ・ |
| ナチの台頭、フィリッピンのドウテルテ、ブラジルのポルソナロなどの強権的政治が |
| 続き、世界は「全体主義」的な政治手法の暗雲に包まれて行くことになるのですが、 |
| アーレントによれば、全体主義は、専制や独裁制の変種でもなければ、野蛮への回帰 |
| でもなく、20世紀に初めて姿を現した全く新しい政治体制だということです。その生 |
| 成は、国民国家の没落、崩壊の歴史と軌を一にしているというのです。 |
| WASP(W=White、白人、AS=Anglo-Saxon、英米人の元であるアングロサクソン民族 |
| に、P=Protestant、英国から海を渡った新教のプロテスタント派の反カトリックの清 |
| 教徒)の国アメリカ合衆国が、1960年代以降段階的に内部崩壊していくことで、「中 |
| 心」も「プロジェクト」も失った「帝国」として出来上がってしまったことに端を発 |
| しているのです。その帝国はその結果、極端な言い方をするなら、パワーと暴力だけ |
| を本質的な価値とするような、(人類学的な意味では)文化を持たない集団によって |
| 率いられる、軍事的でしかない組織となってしまった。これが現在のアメリカ合衆国 |
| なのです。一般的に言えば、従って国家ではなく、「ネオコン=Neoconservative,新 |
| 保守主義者集団」と呼ばれる集団であるにすぎないのです。 |
| 現在のアメリカにおけるトランプ現象、イギリスにおけるEU脱退(プレグジット)、 |
| 欧州における極右や自国中心主義の台頭、米中対立、ウクライナ戦争等々の多くの混 |
| 乱を目の当たりにしています。こうした激変は、単発の事象がランダムに発生した結 |
| 果なのではなく、背景には共通の現象即ち新自由主義(ネオリベラリズム、Neoliber |
| alism)への反乱・反発によるものとわかってきました。 |
| この現象を端的に纏めるなら、1930年代以降の世界システムの支配的な世界観であ |
| った「大きな政府」への挑戦として始まり、1971年のソ連崩壊を機に、新しく世界の |
| 標準システムとして受け入れられるようになった「小さな政府」の価値観への大きな |
| 変化なのです。政府の意思決定や役割を縮小し、市場原理、民間企業や個人の意思・ |
| 判断・選択・裁量をより重要視しようとするものです。例えば、各国別の政府の通商 |
| 政策に代わるものとしてルール・ベースの貿易を促進するためにWTO(World Trade |
| Organization,世界貿易機関)が1995年に作られたとかが挙げられます。この動きは |
| 新自由主義的な価値観を現実化するためのメカニズムであったわけです。この新自由 |
| 主義は、性別、人種、国籍など属性の異なる各個人が、市場を通じて、世界中から自 |
| 由に参加するシステムを目指しますので、より平等で、民主的な世界を目指す価値観 |
| と成る筈でした。何故なら、マイノリティの尊厳も、権利も機会も尊重され、実際に |
| 1990年以降急速に浸透したのでした。 |
| しかし、近年新自由主義に対し世界各地で、強烈な反発が巻き起こっています。新 |
| 自由主義の世界観は信認を失い、既存システムが大きく揺らぎ、機能しなくなってき |
| たのです。このことを理解すると、最近のトランプ現象やプレグジットのみならず、 |
| 米中対立やウクライナ戦争を防ぐ共通した方策が見えてくると思われます。その病根 |
| は従って、今まで世界の行動規範と見做されてきた新自由主義的価値観の崩落だった |
| のです。 |
| | | |
|---|
| 4.おわりに |
| 新自由主義は、しかし、つねに改革を訴え、個人や企業に対しても市場でのたえざ |
| る競争と自己革新を求めるため、社会的格差は、市場での競争の結果として当事者の |
| 自己責任とされます。さらに、格差拡大による福祉・教育・犯罪などへの社会不安さ |
| えも、新たな市場として新自由経済へ組み込もうとするために、正面切って新自由主 |
| 義に根本的な批判をすることが困難でしたが、上記のように、新自由主義的価値観が |
| 崩落するに及んで事情が大きく変わろうとしています。 |
| わが国でも、中曽根康弘内閣から「大きな政府」から「小さな政府」への移行の具 |
| 体策として従来の国有鉄道の民営化、電信電話公社の民営化、郵政事業の民営化、道 |
| 路公団の民営化など多くの基幹的な産業・公共事業が民営化されましたが、これらの |
| ために多くの問題や矛盾が現在では顕在化しつつあり、その対応・解決が難しい社会 |
| ・経済上の問題となってきています。地方山村の過疎化、高齢者の足となる交通網の |
| 縮小やカット、都市と山村の所得や労働対価の格差、常勤と非常勤の労働者の賃金格 |
| 差等々これから解決しなければならない課題も多く、今年のこれからの中央の参議院 |
| 議員選挙や知事や市長、地方議会議員の選挙の結果次第ではさらに大きな変革が顕在 |
| 化することでしょう。 |
| 現に冷戦期にヒーローであったNATO(北大西洋条約機構)も新自由主義の時代には |
| 難しい立場に追い込まれましたが、ロシア・ウクライナ戦争の勃発とともに、NATOの |
| 価値も急騰し、冷戦期には加盟していなかったスエーデンやフインランドまでもが加 |
| 盟を請うようになったのです。言い方を変えるなら、新自由主義の時代では、人々の |
| 世界観は経済が最優先事項でありましたが、現在の全体主義まがいの時代にあっては、 |
| 人々の世界観では地政学が最優先課題となるのでしょうか。アメリカがカナダをアメ |
| リカの州にしようとか、グリーンランドを現在のデンマークからアメリカの領土にし |
| ようとか。中国が日本の沖縄県や鹿児島県の奄美諸島を中国領土に狙っているとか。 |
| また嫌な時代を迎えそうですね。でも、日本もまたアジア地域のリーダーになる余地 |
| もたくさんあるように思われます。 |
| 了 |
| 2025年7月7日 (月)七夕の日に記す |
| | | |
|---|
| 1.はじめに |
| アートの語源はラテン語の“アルス(ars)”で, 現代でいうアート=芸術だけ |
| でなく、「技術」や「技巧」の意味も含んでいました。それが証拠に、英語で文科系 |
| の大学卒業生即ち学士のことは“バッチェラー・オブ・アーツ(Bachelor of Arts)” |
| と呼び、日本語で言うなら人文学のみならず社会学全般をカバーしています。そして |
| ラテン語のアルスの源はプラトンやアリストテレスの哲学と深く結び付いています。 |
| そこで、「哲学的思考を鍛錬するためにアートを理解することが欧米のエリートの |
| 教養の必須要件」となったのです。アートの神髄を知ることは従って、国を知ること、 |
| 民族を知ることであり、これを学び通じるようになれることができて初めてコミュニ |
| ケーションができ、相手の心を動かす影響力を持ち、相手に考えを改めさせたり、受 |
| け入れさせたりすることができると考えられているのです。 |
| アートの感想が感性に対応して「素晴らしいです」とか「涙が出ました」などとい |
| う答えは、本当の答えではなく、単なる反応だけになるのです。感想は、いろいろ湧 |
| いて出た考えやこれからの進め方や対応方法について、参考になること、意欲を掻き |
| 立てられたこと等、具体的な行動として実現したいことへの反応が必要だろうと思い |
| ます。 |
| | | |
|---|
| 2.リベラルアーツとは何か |
| リベラルアーツとは本来いろいろ種類の異なる分野を横断した基礎知識・教養を指 |
| す概念で、日本のビジネス業界でもここ10年ほど特に注目されていますが、その起源 |
| は古代ギリシャ・ローマ時代にさかのぼります。イギリスのカレッジ(College)、 |
| スペイン語のコレヒオ(Colegio)」と呼ばれる「学寮」はその流れを汲みながら、 |
| 今日もリベラルアーツがごく当たり前に日々の活動に溶け込んでいます。 |
| 筆者が今までに訪れた外国152ヶ国での国際会議、日本国の機関や出先の代表とし |
| ての単身での3ヶ月にも及ぶ長期の市場調査、留学、業務上の出張、海外駐在員事務 |
| 所の責任者として現地の人々との会議、会食、その他業務外の自由な会合で非常に役 |
| に立ったことは、アートの世界にかなり突っ込んだ話し合いができたことでした。歴 |
| 史上の画家の作品に対する意見や感想、評価、音楽や文学作品についての感覚的な認 |
| 識の交換、自分で描く作品、書く文章・詩歌等の作品に対する心構え等々、また、飲 |
| むこと、食べることについても好き嫌いや当日の料理に対する率直な意見等々、毎日 |
| の生活にまで及んで人間生活に関係するアートの世界観が大事な意見交換、更には幅 |
| 広い会話の柱になることが経験的によく理解できたのでした。 |
| もし一言も言葉を挟めないようでは話が先に進みませんし、その場だけでなく、そ |
| の後の付き合い全般にわたって肩身を狭くしてしまい、立場が難しい局面に追い込ま |
| れてしまいますので、「何事でも知らないと恥をかく」と精進したくなってしまいま |
| す。これが海外の生活から学んだ日本国内での生活との一番大きな違いでしょう。お |
| 陰で、全世界の著名な美術館、博物館、オペラハウス、競技場、野球場、コンサート |
| ホール、の殆どを訪れることができましたし、有名な作品に接し、マドンナの声を聴 |
| き、ニューヨーク、シカゴ、デトロイト、サンフランシスコ等々での大リーグの名物 |
| カードの試合をネット裏の特別企業の貸し切り特等席で名物料理を食し、美味なカク |
| テルや地元の酒を口にしながら勝負を鑑賞できました。将来のためにその土地その土 |
| 地の特別なものを食べることも進んで行いました。 |
| イギリスのパブではどう振舞うのか、オランダのへリング(ニシン)はどうやって |
| 食べるのか、ニューヨークのオイスター・ベイの観光船上のオイスター(牡蠣)料理 |
| はどういうものがあるのか、ニューヨーク他の米国の鉄道の駅にあるオイスター・バー |
| ではどう振舞うのがベストか、スペインのボデガ(Bodegon)居酒屋の梯子飲み歩き |
| の仕方は、イタリアのバールの過ごし方は等々本当に数多くの経験を積んだことでし |
| た。経験し学んだことで重要なことは、それらについての考え方が、押し売りされた |
| 他人譲りのものではなく、純粋に自分のものになっていて、それを自信をもって、堂々 |
| と自分の口から出せるかに懸っていることです。 |
| | | |
|---|
| 自分が必要とする物を自分で作り、賄い、蓄える ことを自給自足言いますが、こ |
| の熟語は勿論皆様良くご承知の通りです。では「自足の思想」とは何のことでしょう |
| か? |
| この言葉は、料理研究家の土井善晴さんが、新潮文庫に収められている著書「一汁 |
| 一菜でよいという提案」の中で述べられている、以下のような絶妙な文章を読まれた |
| 解剖学者で趣味の昆虫の分野でも多くの話題を提供されている養老孟司さんが、新潮 |
| 社から最近出された著作「人生の壁」(新潮新書、2024年11月20日初版刊行)の中で |
| 参照されたその文章に対して冠せられた言葉です。土井さんの文章は、「暮らしにお |
| いて大切なことは、自分自身の心の置き場、心地良い場所に帰ってくる生活のリズム |
| を作ることだと思います。その柱となるのが食事です。」と綴られています。 |
| 養老さんは、ご自分で冠せられた「自足の思想」のことを次のようにご自分の著作 |
| 「人間の壁」の中で説明しておられます。「つまり、自分自身が幸せな状態をつくる |
| のが一番であり、大切なことであるという考え方です。政治や社会に関する大きなテ |
| ーマを考えるにしても、個人のレベルで基本にすべきことは、この考え方ではないで |
| しょうか。自分にとって居心地のいい状態を知っておくのはとても大切です。これを |
| 誰もができているとは限らない。自分自身の限界とも関係するため、見極めるのが難 |
| しいのです。」 |
| *筆者注:自足とは「自分で必要を満たすことのできる」という意味で、英語で言 |
| うなら“Self-sufficient”となるのでしょうか。 |
| 筆者は養老先生の著書は殆ど読ませていただいていますが、「xxの壁」シリーズ |
| の中でもこの「人生の壁」のこの件(クダリ)が一番好きです。勿論この通りできる |
| ことは理想でしょうが、自分がそれまでにどれだけ努力し、精進したかでその実現は |
| 決まることでしょう。目標が大きくてもしっかりしていることは大切なことだと思い |
| ます。 |
| ご自分の考え方を専門の分野の例でうまく表現される土井先生の展開方法も素晴ら |
| しいと思いますが、その文章に共鳴・共感されて、それを礎にご自分の考えをしっか |
| りとしたテーマに描いて表される養老先生の心意気には、それ以上の感激と読書の醍 |
| 醐味を感じないでは済まされない気持ちです。 |
| いずれにしても、今回は紹介のみに留めさせてもらいます。 |
| 了 |
| 2025年6月18日(水) 記 |
| | | |
|---|
| 3.日本語がすっかり変わってしまった |
| 何か別のテーマの際、ちょっと書いたように思いますが、日本には言葉のアカデミー |
| というか、国の監督機関がありません。他の先進諸国には、新しい言葉やその言葉の |
| 及ぶ範囲をあらかじめ軽く規定していますので、特に外来語に対してどのような訳語 |
| を当てるかを一般国民にまで知らせているのですが、残念ながらわが国にはそのよう |
| なアカデミーもなく、近年特に外来語がそのままカタカナで発音通りに置き換えられ |
| て使われたり、二つ、三つの言葉から成るものは、その頭文字だけを取って並べる例 |
| えばIMF(International Moneytary Fund 国際通貨基金)のようなやり方が大流行で、 |
| デジタル技術の浸透と共に、更にホームページ、Myページ、ライフプラン、コールセ |
| ンター、タブレット、確認サービス、ログインパスワード、ダウンロード、オンライ |
| ンサービス、QRコード、バンキングアプリ等々枚挙にいとまがないくらいたくさんの |
| 言葉が特に誰の許可も制限もなく使われており、まだ辞書にも登場していない言葉も |
| 少なくないと思われます。この有様では関係する業界や製品に馴染みのある人なら兎 |
| も角、直接関係のない人々や既に仕事から遠退いて久しい高齢の人々には何のことや |
| らさっぱり分からず困っている方々がさぞかし多いことかと推察されます。 |
| 言葉それ自体独り歩きする性格のものですが、もう少し範囲を決めるなり、用例を |
| 統一するなり、一定の規則があっても良いのではないかと考えるのです。改めて言葉 |
| のアカデミーを持つことを提案したいと思います。 |
| | | |
|---|
| 2025年上期の芥川賞、直木賞は審査員の激論の末、該当作なしと異例の展開となり |
| ました。候補作4点は、いずれも意欲的でしたが、「文学史に残る可能性」や「独創 |
| 性」「深み」がもう一歩足りなかったと評価されました。妥協を許さない、業界に配 |
| 慮しない厳しい評価のようです。 |
| 以前、佐藤 雅寿さんが紹介された、河田博士の銀華文学賞の小説を思い出しWEB |
| 検索したところ、文芸思潮WEB版でバックナンバーとして公開していました。内容は、 |
| 1954年(昭和29年)日本航海計器の若き技術者の体験談です。 |
| ある日、業務で捕鯨船のオートパイロットの改修作業で造船所に出張しました。改 |
| 修後、予定にない海上試験に立ち会うことになり出航しました。洋上に出ると天候が |
| 急変し、荒れ狂う洋上で過酷な体験をすることになり、生死をさまような苦しい状況 |
| が続きました・・・。審査員から小説の展開と結末が絶賛されています。 |
| “荒るる海”は文語的、古典表現で、現代語では“荒れる海”と書くそうです。細 |
| 部にわたり技術的裏付けがあり関係者にしか理解出来ないか、と思わせる内容ですが、 |
| 文学の専門家からも高く評価される強烈な“何か”があるようです。銀華文学賞は芥 |
| 川賞などのプロ作家の登竜門や格付けではなく、熟年シニア層の文学創作意欲を推進 |
| する奨励機能を目的にしているようです。主人公の内面や人間関係の機微を丁寧に掘 |
| り下げる作品が評価されやすいそうです。 |
| 私は、何を意図しているか分からない高度に難解な文学より。人それぞれ異なると |
| 思いますが、自分のこころに響く小説の方が感動します。「荒るる海」は価値ある名 |
| 作と確信しました。 |
| | | |
|---|
| 若いと思っていましたが、私も80歳の大台になりました。そして数年前から段々耳 |
| が遠くなり、大勢での会話やテレビの音声が聞こえなくなりました。 |
| そろそろ補聴器を買わなくてはいけないかなと思い始めていました。しかし、何十 |
| 万円もする補聴器を作ったが耳に合わないで使っていないという話をよく耳にします。 |
| 私の妻も昔高価な補聴器を作りましたが、装着していません。 |
| 2月に私が80歳になった時に子供が誕生日祝いをしてくれ、その時にプレゼントし |
| てくれたのが、「Air Pods Pro」というApple社製のイヤホンでした。 |
| 「最近耳が遠くってなかなか話がうまく通じないので、使ってみたら」と子供に言わ |
| れました。そしてこのAir Pods Proという補聴器をつけてみたら、今までの難聴の状 |
| 態が大きく改善したのです。このAir Pods Proは何もしないで耳につけても何も改善 |
| されません。前もって操作が必要です。 |
| iPhoneとAir Pods Pro をblue toothで接続して、イヤホンを耳に装着してiPhoneに |
| 入力されたAir Pods Proを使用するためのソフトをblue toothから起動します。する |
| とガイドが出てきますので、それに従って進めます。これは聴力検査をして、自分の |
| 聴力に合わせる調整です。 |
| 私は両耳とも中程度の難聴という結果でした。これを付けたら今まで音量25でも聞 |
| こえなかったテレビが15でもはっきり聞こえるようになりました。また会議などで聞 |
| こえなかった会話が普通に聞こえるようになりました。補聴器を作ろうかどうか悩ん |
| でいましたが、高い買い物をしなくて済みました。 |
| 高い補聴器を買って、使い難いといって使用していなかった妻にもAirPods Proを購 |
| 入しましたが、補聴器よりも快適のようで、普段持ち歩いています。 |
| 私は自分では購入していませんが、アップルに店で娘は36,000円で購入したようです。 |
| 聴力検査ではスマホのiPhoneを使いますが、調整後はiPhoneがなくても補聴器として |
| 機能します。以下がセットするときの概略の手順です。 |
| (1)Air Pods Proを購入する |
| (2)iPhoneとblue toothで接続する。(スマホの「設定」からblue toothに進む) |
| (3)イヤホンを耳に装着する |
| (4)blue toothと接続したら表示されているblue toothのメニューに表示されている |
| 「Air Pods Pro」を起動する(Air Pods Proと表示されている右にある〇i(〇の |
| 中にiが表示されている)をタップする) |
| (5)「Appleのヒアリングチェックを受ける」をタップする。 |
| 以降表示される手順に従って進むと自分の聴力をチェックし、耳に装着した補聴器 |
| (イヤホン)を自分の聴力に合わせてくれる。 |
| その後分かったことですが、Air Pods ProはiPhoneとしかblue toothで接続できな |
| いようですが、最近類似品が出ていますので、スマホがiPhoneではない方はそちらを |
| 調べてみてください。 |
| これで終わりです。ぜひお試しください。耳寄りなお話しでした。 |
| | | |
|---|
| 2.自分のことは本人が一番分かっていると思うことが過ちの元 |
| ~自信と自己中心主義の振る舞いとの混同は避けよう~ |
| 日頃の生活の中で、良く周囲の人から意見を言われたり、忠告を受けたりすると、 |
| 「余計なことを言うな!! 自分ことは俺が一番よく知っている!」と反発して答え |
| たり、もっと言葉を足して反論したりすることが多いかと思われますが、これが実は |
| 大きな間違いであり、過ちで、大きな解決の道を提案されたにも拘らず、考慮に入れ |
| ることもせず、謙虚に一度自分の心の中に取り入れて判断、熟慮してみる機会を逸し |
| てしまっていることに気付かずに済ませてしまっているのです。実際には、自分のこ |
| とが分かっていない人が殆どいうか、むしろ当たり前なのです。自分の理想とするこ |
| とと現実とのギャップがどのくらい差異があるのかが自分では理解できないからです。 |
| この意味で、こういう場合に謙虚に耳を傾けられるか否かが、次の場面の大事なアク |
| ションに繋げて行くために大変必要なことだと思うのです。もう少し極端に言うなら、 |
| むしろ逆に友人や周囲の人々で、自分のことをよく理解してくれている人々の意見、 |
| 忠告、提案、諭しの中に、最も大切な核心を突くものが潜んでいると斟酌してみるこ |
| とが重要でしょう。 |
| 仕事上でも、家庭での例えば子供の教育や将来の構想に悩みや迷いがあれば、専門 |
| の第三者や親しい友人にそれとなく相談し、意見を求めるでしょうが、それはその人 |
| の意見を拝聴して、自分の考え方の正否はおろか正しく自分なりに納得のいく結論を |
| 出したいからでしょう。何はともあれ、相手の言い分を聞きたいのです。 |
| | | |
|---|
| 3.真摯に耳を傾けよう、そして自分をアップデイトさせよう |
| このように、特に自分の最終判断の上には、周りの人の意見や主張に真摯に耳を傾 |
| けることがなくてはならない重要な段階であり、聞くことが大事になってきます。さ |
| らに付け加えるなら、いつも同じ人の意見ばかりを頼りにすのではなく、出来れば複 |
| 数の異なる環境の人々の意見を聞くことが必要でしょう。特に企業・団体には特有の、 |
| そして固有のミッションやビジョンがあり、自分がそこに属しているときには、それ |
| と自分の考えていることとに齟齬がないことも求められる大事なことと言えるでしょ |
| う。 |
| これら企業・団体のビジョン、ミッションは常にアップデートされていますので、 |
| その構成員たる個人もまた「何をしなければならないのか?」、「どう改善したり、 |
| 重厚にしたりすることが必要であり、望まれることか?」を自分の心にしっかり持ち、 |
| 毎日の生活の態度としてシンクロナイズできるよう、アップデートしておく必要があ |
| ります。周囲の意見が十分に収集、聴取できて、帰属している母体や社会と同じベク |
| トルで進める態勢になっていることが求められるでしょう。 |
| 極端に言うなら、昨日までの自分と今日からの自分は同じではなく、正しく前進で |
| きていなくてはならないでしょう。自分のしっかりした間違いのない、正しい結論に |
| 基づいた努力と反省がシンクロナイズされたポジション・セッティングとマインド・ |
| コントロールを生み出すものとして要求されるでしょう。 |
| | | |
|---|
| “ワインにはカロリーがある。栄養素がある。香りがある。 |
| アルコール飲料としての潜在能力は、フランス人の考えでは |
| (あるいは飲むときには)あまり重視されない。たいていのフ |
| ランス人はワインを聖なる贈り物だから、むだにせずに楽しむ |
| べきだと考えているのだ。フランスの詩人ボードレールは、人 |
| 間の作り出したものからワインが消えたら、人間の健康と知性 |
| に大きな穴が空いてしまう。そして、その人は罪悪感を覚える |
| あらゆる不摂生よりも始末に悪い、と言っている。ワインは五 |
| 感を自覚させるために飲むものである。そしてそれは食べ物を |
| 楽しむためにはきわめて重要なことである。” |
| さらに、同氏は続けて以下のように綴っている。 |
| “毎日少量ずつ、常に食物といっしょに飲めば、ワインは健 |
| 康にも役立つ。なお、フランス女性は、カクテルのようにシャ |
| ルドネのワインだけをちびちびすすっているのは実は奇妙だと |
| 考えている。ワインの完全な味は、しかるべき食べ物と組み合 |
| わされた時に初めて発揮されるのだ。たいていのアルコール飲 |
| 料よりもカロリーが少ないだけでなく、上等なワインは栄養素 |
| に富み、血液をサラサラにして、血圧を下げ、悪玉コレステロ |
| ールを減らす効用がある。心から楽しめるばかりか、そういう |
| 効能のあるものが他にあるだろうか?” |
| | | |
|---|
| 2.では、何故この期に及んでスマホなどと? |
| ずっと使い続けてきた3台目のパソコンが昨年9月末に動かなくなって、自分の歳 |
| を考えて、さらに新機種を入れるか否かを悩んでいたところ、ガラ系を最後に携帯電 |
| 話も持っていなかったために、気が付けばコミュニケーションの手段が定置電話のみ |
| となってしまい、不便で仕方ありませんでした。そこで、まだ暫くは生き延びられる |
| であろうと仮定して、もう一度だけPCとスマホの両方を調達することに決めたのでし |
| た。 |
| でも、スマホを入手したはいいが、複雑すぎて何が何やら思うに任せず、仕方なく |
| 教室に通うことになった次第です。結果として、スマホ本体の価格は驚くほどではな |
| かったのですが、教室の受講料や教材費を足すと何倍かに膨れ上がってしまい、収入 |
| のない今のわが身には過ぎた試みであったと一時反省の毎日でした。 |
| 更にびっくりしたことには、新しく入手したノート型パソコンに電源を入れて最初 |
| に現れる画面が以前のパソコンとは全く違った、どちらかと言えばスマホに共通のマ |
| ーク、記号表示でした。スマホ教室に通っていて少しでも画面に表示されている諸々 |
| のマーク、記号、言葉に慣れていて良かった!!と、しみじみ思ったことでした。暫 |
| く接していない間にかくも大きな変化が起こっており、ある種の恐ろしさと進歩のス |
| ピードに驚きを禁じ得ませんでした。 |
| | | |
|---|
| 3.今迄できていたことができなくなった不便 |
| スマホやパソコンを持っていなくともできていたことが、最近になってできなくな |
| って不便を感じることが多くなってきました。従来郵送や電話で確認したり、情報交 |
| 換をしていたことが、一方的な通告により、ある日を境にしてできなくなり、それら |
| の行為はスマホ、パソコン或いはQRの読み取りによってのみ可能ということが多くな |
| ってしまいました。例えば、毎月その前月にクレジットカードを使って買い物をした |
| り、支払いをした金額が指定の銀行口座から引き落とされる前に貰えていた計算書や |
| 通知書が自動的には貰うことができなくなり、対価や手数料を支払うことを事前に約 |
| 束した場合のみ以前と同様の計算書や通知書を入手することができるといったやり方 |
| に変わったことなどです。また、クレジットカードを使って電話で買い物をすること |
| も、デパートや大手の商店では出なくなって、ついつい面倒くさくなり止めてしまう |
| ことが多くなってきました。 |
| 卑近な一例を申し上げるなら、2025年4月からオンラインショッピングで従来から |
| 持っているメンバーシップのカードを使おうとするなら、その前に本人の認証サービ |
| ス(3Dセキュア)の設定が必要となったことです。特に、クレジットカードの不正 |
| 利用による事件の発生が最近の4年でそれまでの倍にもなっているそうで、その防止 |
| 策として考えられたことのようですが、まず本人はおろか万一カードが家族も使える |
| ようになっているなら、関係する全員のカードのWeb会員登録を先ずしなければなりま |
| せん。高齢アナログ人間には、直ぐに「あゝ、そうですか!ハイ!」とアクションに |
| は移せないのです。 |
| 日本が世界の国々に比較してデジタル化が遅れていますので、それを取り戻すため |
| に、いろいろ作業を進めることが必要ですが、今までデジタル製品を扱い慣れていな |
| い、或いは人によっては一度も手にしたこともない高齢者はどうすればよいのでしょ |
| うか。一足跳びに従来のマニュアルやアナログのシステムからデジタルのシステムに |
| 移行するのではなく、軟着陸の移行期間を設けて、慣れるまでの猶予期間を事前に通 |
| 告の上作って欲しいと願いたいのです。 |
| 蛇足ながら、良い機会なので一言付け加えさせてもらえるなら、最近の作家先生方、 |
| 特に男性の作家さんには理科系出身の方々が多いためか、スマホやパソコン、その他 |
| デジタル機器が小説の中でも大きな役割を演じているように思われます。あながち筆 |
| 者の偏った思いでもなかろうかと思いますが・・・・。 |
| | | |
|---|
| 1.はじめに |
| 本日、3月7日の誕生日で筆者も到頭米寿を迎えることとなってしまった。これま |
| での人生を振り返ってしみじみ人生には良い思い出、誇れる思い出の数々が如何に大 |
| 切かを思い出させてくれる。何故なら人生で一番大切な仕事は自分の人生を飾る「思 |
| い出作り」だと思うからである。その人がどういう人生を送ったかを振り返るときに |
| は、その人が毎日、毎週、毎月、毎年どういう経験を積み重ね、自分を形成し、住ん |
| だ地域社会、在籍した学校、企業や団体に有形・無形の寄与・貢献を成し、その人に |
| しか成し得なかった一生に一度の経験を見れば、自然にその姿が偲ばれると思うから |
| である。 |
| これらの思い出や経験を成すに当たっては幾つかの重要な要素が絡んでくると思わ |
| れるが、それらの中でも最も大きなウエイトを占めるものは筆者は自分の人生を顧み |
| て、好奇心であり、その有無とその大小ではなかろうかと思う。特に幼・少年期の好 |
| 奇心は、その人のその後の人生を形作る基本的な、一番大事なファクターであると言 |
| っても過言ではあるまいと思う。 |
| 我々の住むこの地球の生い立ちや今後の発展、更には宇宙への進出等を考えてみて |
| も、関係する諸科学は尽きることのない多くの人々の好奇心と共に発展し続けること |
| だろうから、先ずは個々人の考えが如何に効果的に結び付いて、大きな学術的な力に |
| まで発展できるかの勝負だろうと思う。 |
| | | |
|---|
| 2.好奇心と計画性 |
| 以下述べることは筆者独自のまったく異例の事になるかも知れないが、好奇心が湧 |
| くと何等かのアクションをしようとして短期或いは長期の差はあっても、何等かの好 |
| 奇心の実現の仕方、極め方を模索して幾つかの道筋や方法論を見付けようとしてきた。 |
| あまりよい例ではないが、筆者が学校に上がる前、昭和16,17(1941,42)年頃は |
| いわゆる第2次世界大戦の最中で、一般家庭用に使える防腐剤、殺虫剤など乏しく、 |
| 庭木には毒毛虫が湧くように発生していた。その中にマツケムシ(松毛虫)と呼んで |
| いた首筋に首輪のような青紫色の帯を持った毛虫がおり、その毛先に触れようものな |
| らボツボツの赤い斑点が出来て、腫れて大騒ぎになっていた。そのとき、筆者は何故 |
| か毎日割箸で枝葉の毛虫を摘み取り、缶詰の空き缶の中に入れて平たい石を重しにし |
| て殺すのがお手伝いの一仕事であった。以来どういう訳か昆虫に興味と関心が向き、 |
| 小学校6年生で東京に戻るまで福井県の父の郷里の山里に4年間疎開していたが、そ |
| の間あらゆる昆虫を手にし、標本に作り、自然との親しみを満喫したのであった。興 |
| 味は昆虫だけでなく自然に他の動植物にも及び、家畜や野獣等の多くの動物、鳥、魚、 |
| 食べられる山の木の実等々を含め山野草に至るまでの名前を覚えることができた。お |
| 陰で以後高校、大学を通じ、課外活動として生物部や生物研究会に所属し、リーダー |
| として活動することになってしまった。この自分史を顧みて、好奇心がしばしば計画 |
| 性を伴うものだと思わずにはいられなかった。 |
| この事の発端になったことは、高校に入学して通学に片道1時間以上も費やす時間 |
| が勿体なく思い、一念発起して卒業までの3年間に当時発行されていた岩波書店と新 |
| 潮社の世界と日本の文学の文庫本全冊の読破を計画し、2~3日で1冊を読み上げる |
| スピードで3年を待たずに制覇し、余った時間をクラスメートの親が趣味で持ってお |
| られた改造社のA5版くらいのクロス表装の世界文学全集を週に2~3冊借りてそれら |
| も全冊読了してしまった。また、自分としても文章を綴りたくなり、機会ある毎にペ |
| ンや鉛筆を走らせている自分を見付けることができるようになった。以来文学に親し |
| み、文章や語彙に関心が向いて、方言や外来語、漢詩に至るまであらゆる文章や書物 |
| を乱読して今日に至っている。 |
| | | |
|---|
| 1.はじめに |
| 2023年3月米国の女子高生ネキャ・ジャクソンとカルセヤ・ジョンソンが驚くべき |
| 成果をジョージャ州アトランタで開催された米国数学会の地域会議に発表した。 |
| その内容は、“三角関数を用いたピタゴラスの定理の証明”だった。 |
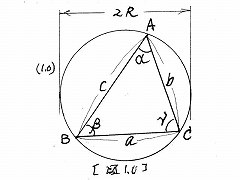
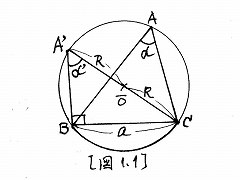
| 周知のように、図1に示す直角三角形の3辺a,b,c の間に成立する次式: |
| a^2+b^2=c^2 , (1) |
| がピタゴラスの定理であり、我国では三平方の定理と呼 |
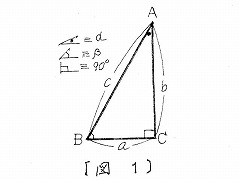
図1 |
| んでいる。 |
| このピタゴラスの定理は、BC500年頃から知られてお |
| り、現在まで多数の数学者により実に100通り以上の証 |
| 明がなされているが、これらのほとんどが幾何学または |
| 代数学を使用しており、三角関数によるものは知られて |
| いない。これは三角関数に関する定理にピタゴラスの定 |
| 理に立脚したものがあり、「循環法」に陥る恐れがある |
| からだと思われる。本レポートで紹介する証明は、三角関数と無限等比級数を使用して |
| いるが、ピタゴラスの定理と無縁な定理だけを使用しておるので循環の恐れがない。こ |
| れを明確にする目的で、本レポートで使用する全ての定理を証明し、Appendixに記載し |
| て置く。 |
| [注記]:文章中の数式表記 |

|
| | | |
|---|
| 3.証 明 |
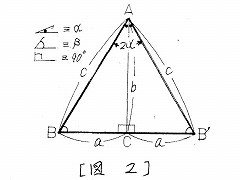
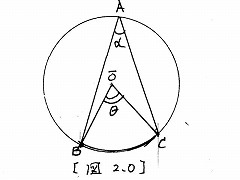
| 図2に正弦定理(A1参照)を適用し、次式: |
| 2a/sin2α=c/sinβ, (図2参照), (2) |
| を得る。上式中のsinβは、定義により次式: |
| sinβ=b/c, (図2参照) (3) |
| なので、これを(2)に代入して下式を得る。 |
| 2a/sin2α = c/(b/c) |
| ∴ sin2α=2ab/c^2, (4) |
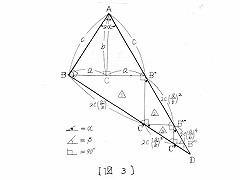
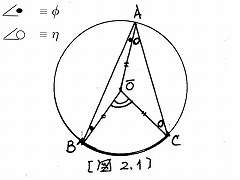
| 次に、図3を使用する前にこの図がもつ性質を明らかにしておく。 |
| 三角形△1,△2,△3,・・・の内角が△ABCのそれと等しいので |
| ・△ABC,△AB'C,△1,△2,△3,・・・が互いに相似である。 〈1〉 |
| また、α+β+90°=180°∴α+β=90°なので |
| ・大きな三角形ABDの角(ABD)=90° である。 〈2〉 |
| 三角形ABDで〈2〉が成立するので、sin2αは次式: |
| sin2α=BD/AD, (∵sin2αの定義), (5) |
| で与えられる。 |
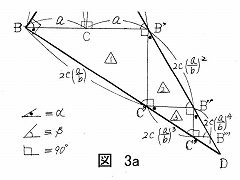
| 次に、小さい三角形△1,△2,△3,・・・の各辺を〈1〉を利用して求める: |
| BC' /BB' =c/b, ∴ BC’=2c(a/b), ∵ BB’=2a, (6) |
| B'C'/BB' =a/b, ∴ B'C'=2a(a/b), ∵ 同上, (7) |
| B'B''/B'C'=c/b, ∴ B'B''=2c(a/b)^2, ∵ (7), (8) |
| B''C'/B'C'=a/b, ∴ B''C'=2a(a/b)^2, ∵ (7), (9) |
| C'C''/B''C'=c/b, ∴ C'C''=2c(a/b)^3, ∵ (9), (10) |
| B''C''/B''C'=a/b, ∴ B''C''=2a(a/b)^3, ∵ (9), (11) |
| 以上より、大きい三角形の一辺BDは、次式で計算される。 |
| BD=BC'+C'C''+C''C'''+・・・, (図3参照) |
| =2c(a/b)+2c(a/b)^3+2c(a/b)^5+・・・, (12) |
| BD=2c(a/b){1/(1-(a/b)^2)} (∵等比数列の和の公式[A3参照]による) |
| =2abc/(b^2-a^2), (∵ 0<(a/b)^2<1 ), (13) |
| 大きい三角形の他の一辺ADは、次式で表される。 |
| AD=AB'+B'B''+B''B'''+・・・, (図3参照) |
| =c+2c(a/b)^2+2c(a/b)^4+・・・ |
| =c+2c(a/b)^2{1/(1-(a/b)^2)}, (∵ (a/b)^2<1 ) |
| ={(b^2+a^2)/(b^2-a^2)}c, (14) |
| (13)と(14)を(5)に代入し、次式を得る。 |
| sin2α={2abc/(b^2-a^2)}/{((b^2+a^2)/(b^2-a^2))c} |
| =2ab/(a^2+b^2) , (15) |
| この(15)と(4)より次式を得る。 |
| 2ab/c^2 = 2ab/(a^2+b^2) =sin2α, (16) |
| 故に、ピタゴラスの定理: |
| a^2+b^2=c^2 (17) |
| が得られる。 <証明完了> |












 をクリックすると記事詳細が表示され、
をクリックすると記事詳細が表示され、
 をクリックすると予定・報告の一覧表に戻ります。
をクリックすると予定・報告の一覧表に戻ります。 は、クリックすると図や写真が大きく表示されます。
は、クリックすると図や写真が大きく表示されます。