| �b�@��@�w�@�����ܘb�@�x�ŐV | 2017�N1���`2017�N4�� | |
| �@�@�@�@�@�@�@�@�@�@�b�@�@��@�@��@�@�� |
| 2017. 9.20 | �V���[���b�c�r�������̕ɐڂ��� �@�@�@�@�@���e�F�����L�� |  |
| 2017. 7.29 | �O�����̒藝�Ɋւ�������ܘb�@�@�@�@�@�@�@ ���e�F���c�V�O |  |
| 2017. 6.25 | ���������{�w�I�s�ƴ����œǂލ�Ƃ̎R���x��ǂ� ���e:�����L�� |  |
| 2017. 6. 8 | �ʔ����ǂw���E�V�ˋI�s�x�@�@�@�@�@�@�@�@ ���e�F�����L�� |  |
| 2017. 6. 2 | ���U���Ă��A�Ԑ���I2017�N�ŁF���̂T�@�@�@ �@���e�G���c �� |  |
| 2017. 5.23 | ���U���Ă��A�Ԑ���I2017�N�ŁF���̂S�@�@�@ �@���e�G���c �� |  |
| 2017. 5.10 | �^�e�n�`���E�Ȃ̒��u�A�J�{�V�S�}�_���v�����Ȃ́u����O�������v�ɒlj��w�肳���@�@�@�@�@�@�@�@�@�@�@�@�@�@ ���e:�����L�� |  |
 ���N���b�N����ƋL���ڍׂ��\������A
���N���b�N����ƋL���ڍׂ��\������A
 ���N���b�N����Ɨ\��E�̈ꗗ�\�ɖ߂�܂��B
���N���b�N����Ɨ\��E�̈ꗗ�\�ɖ߂�܂��B
�F�̘g�ň͂܂ꂽ
 �́A�N���b�N����Ɛ}��ʐ^���傫���\������܂��B
�́A�N���b�N����Ɛ}��ʐ^���傫���\������܂��B
| �@�@�@�@�@�@�@�@�@�@�b�@�@��@�@�w�@�����ܘb�@�x | �@ |
| 2017. 9.20 | ���� | �V���[���b�c�r�������̕ɐڂ��� |  |
| �V���[���b�c�r�������̕ɐڂ��� | ���l�s�@�����@�L�� | |
| �@���ʂ̕č����@�[�W�j�A�B�V���[���b�c�r���s�ł̔��l�����`�W�c�Ɛl�퍷�ʔ� | |||
| �Δh�̐l�X�Ƃ̏Փˎ����̕��A�ő��Ƀ}�X�R�~�̘b��ɏ�邱�Ƃ̂Ȃ��n�� | |||
| �����ɁA���s�ɖ{���ƍH���u���Ă����X�y���[�E�}���[���E�V�X�e���X�E�f�B���B | |||
| �W�����iSperry Marine Systems Division�A���́gSMSD�h�j�Ƃ̊Ԃōs���Ă����� | |||
| �Ж���Ə����̔��p�@��A���ɓ����o�^���W�̂悤�Ɏg��ꂽSQMP�iSperry | |||
| Qualified Marine Products |
�č��ާ�Ƽޱ�B���ۯ���َs |
�č��ާ�Ƽޱ�B���ۯ���َs_2 |
|
| �̓��������Ƃ��āg�X�N�C | |||
| ���v�h�Ɣ������Ă����j�} | |||
| ���[���E���[�_�[�A�W���C | |||
| ���R���p�X�A�p�C���b�g�� | |||
| ��OEM���i�̗A�o���i�Ɛ� | |||
| �ʌ�����̂��Ƃ��v���o | |||
| ���ꂽ�B | |||
| �@1950�N�㓖���̓����v��̒�g���SMSD�Ƃ̔N�Ԍ_����ɂ͕M�҂����i�����̈� | |||
| ���Ƃ��đ�ϋ�J������ꂽ�B���i�E���ʌ��ɂ͋ɒ[�Ɍ����A����Ə��̐��� | |||
| �����̑��̉����~�߂��˂Ȃ��ӔC���|�����Ă����̂ŁA���̂��߂ɃV���[���b�c�r | |||
| ����K�˂邱�Ƃ́A�厖�Ȉӎv�\���ƌ��f�𔗂���d��Ȏg����ттĂ����B | |||
| ���v���o���Ă����̌����ꃖ���ȏ�ɋy�Ԃ��Ƃ��������Ȃ��A�M�҂��傫�ȃf�b�h | |||
| ���b�N�ɏ��グ�āA������ÂɂȂ�K�v������Ƃ��āA�r���œ����₷���߂ɋ} | |||
| 篃J�i�_�ɔ�сA��T�Ԃ��炢���_�𗣂�ċC�����ւ��Ă���A���߂Č����ĊJ | |||
| �������ƂȂǂ��v���o���Ă���B���͖S��SMSD�̍w�������z�v�L���X����Ƃ̗F��� | |||
| �x���������l�ԊW�ɂ��T���肻���Ȍ���ʂ̖����ɂ��݂��ɎE���Ȗ����Ɩ� | |||
| ���߂Ȑ��E�����������̂ł������B�����̓��Ћ���@���В��A�����@�B���p���ƕ����A | |||
| ��g�@����Y�C�O�c�ƕ������ӔC�ґS�������ɋS�Ђɓ����Ă��邽�߁A���ʂ̘b�� | |||
| �Ƃ��Ęb�������̃e�[�}�ɂ��邱�Ƃ���ł��Ȃ����݂ł́A�����̓��̈ꎖ���Ƃ��� | |||
| �b��ɂ��邵�����Ȃ����Ƃ͐r���c�O�ȋC������B | |||
| �@�v���Ԃ��A�}���[���E���[�_�[�ȂLjقȂ�@�\�����R���|�[�l���g��g�ݍ��� | |||
| ���ăV�X�e�����`������@��ł́A�e�R���|�[�l���g�̒P���ƃV�X�e���Ƃ��đg�ݏ� | |||
| �����Ƃ��̃V�X�e���E�v���C�X�Ƃ̊W�̐�����������������̂Ƃ��Č��߂邽�߂ɁA | |||
| �r���f�B���O�E�u���b�N�����Ƃ������āA�R���|�[�l���g�P���̐ςݏd�˂ƃV�X�e�� | |||
| �P���Ƃ̐����������߂�w�͖͂��N��ϐS���ӂ�����ۑ�ł������B���Ɍ��݂ł� | |||
| �X�y���[�Ƃ̊W����A���̂悤�ȑS���E��ɂ������i�E���ʌ��̓y�U���� | |||
| �͍~��Ă��邪�A���͉������������̋ꂵ�݂̈�[���v���o���āA�}�炸���ߋ��̗� | |||
| �����i�M�҂͍��ł��ǂ����Ƃ������Ƌ敪�����Ă��邪�E�E�E�j�̎v���o��h�点�� | |||
| ���Ƃ������B�S���E������̃x���g�ɕ����āA���̒n������z����ӔC�҂�u���āA | |||
| ���А��̔��p���i���X�y���[�̃l�b�g�ɏ���đS���E�ɔz�z����čs���p�͌����Ď� | |||
| �Ă����̂ł͂Ȃ��A�������Ƃ��Ă͑傢�ɖ��c��ތ����̔ɉh���f���p�Ƃ��Ċ�т� | |||
| �������v���𖡂킦��ꎞ�ł͂������B�Ɩ�����ĕ��a�𖡂킦��M�d�ȑ̌����� | |||
| ����@��Ă����̂�������Ȃ��B��Ƃ̃O���[�v���Ɗ��S�Ɨ��̂ő�C�̎��R�� | |||
| ���키���Ƃ̌��߂͂����ȒP�ɂ͌��_���o������ł͂Ȃ��낤���A���݂ǂ̎Y�Ƃ� | |||
| ���A�ǂ̍��ɂ����ʂɔY�܂������Ƃ��ĉe�𗎂Ƃ��Ă���̂ł͂Ȃ��낤���B | |||
| �@�Ⴆ�ΐl�Ԃ��t�@�b�V���������邽�߂ɏd�˒������邱�Ƃ��]�܂����̂��A�� | |||
| ���ƊȒP�ɗ��g�ɋ߂��p�ł��A�������܂������R�̂ɂ��̖{���̎p�����߂�̂��ǂ� | |||
| �̂��A�܂��b���c�_�Ǝ��H�̎��s���낪�J��L�����邱�Ƃł��낤���A���g�߂ɁA | |||
| ���ȕւɁA����c�_���o�邱�ƂȂ��A���_�������o�����������߂����Ƃ��݂� | |||
| �ݎv���썡�ł���B����ɂ��Ă��v�l�̉ߒ������̂ɂ��悤�ɕ��G�Ɋ��ݍ���˂� | |||
| ��Ȃ��̂��A�M�҂ɂ͗ǂ�������Ȃ����肩�A�����̋^��ɑΏ����������ᖡ | |||
| ���邱�Ƃɋ�`���₵�A�V���ȓ�������������߂悤�Ƃ���w�͂Ɍ�������邱 | |||
| �Ƃ��ʂ����Đ��������@�Ȃ̂��A�M�҂ɂ͐r���^��ɉf��̂ł���B��͂�A������ | |||
| ������I�ۂł���A�D�����r�𐂂�āA�ӎu��\�����ė~�����Ǝv���̂������� | |||
| �͂Ȃ��낤���B | |||
| �M�҂̈ӂɔ����āA����N�w�ⓚ�ɂ����������ɂȂ��Ă��܂����B�~�߂ɂ��悤�B | |||
| �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�� | |||
| �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@2017�N�W��17���i�j�@�@�L | |||
| 2017. 7.29 | ���c | �O�����̒藝�Ɋւ�������ܘb |  |
| �O�����̒藝�Ɋւ�������ܘb�@ | ������s�@���c�@�V�O | |
| �P.�@�͂��߂� | |||
| �@�͂��߂ē��e���܂��B���G���W�j���̊F�l�ɓǂ�ł��炦�����ȋL���������Ă݂� | |||
| �����B��������Ƃ̉�b�̃l�^�ɂł��Ȃ�K���ł��B | |||
| �Q.�@���̂ɂ��� | |||
| �@���O���ł́u�s�^�S���X�̒藝�i�p�FPytagorean�@theorem�j�v�ƌĂ�ł���̂ɁA | |||
| �Ȃ��䂪�������u�O�����̒藝�v�Ə̂��Ă���̂ł��傤���B | |||
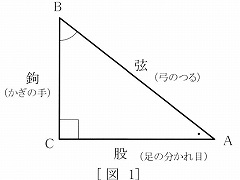
�}�P_��Ҍ��̖@ |
�@�̘̂a�Z�ł́A�����ɂȂ���āu��Ҍ��̖@�i������ | ||
| ����̂ق��j�v�Ə̂��A�ق��������(�������킹���� | |||
| ����)�̈�Ƃ��Ď��グ�Ă����悤�ł��i�}�P�Q�Ɓj�B | |||
| ���̌㖾���ɓ����āA���O���ɍ����āu�s�^�S���X�̒� | |||
| ���v�ƌĂт������̂ł����A����E��풆�ɁA�G�� | |||
| �ꂪ�ւ����A�������̂������A�����Ȃ̐}���ďC���� | |||
| �Ƃ߂Ă������쒼���i������ �Ȃ��݂�1893 - 1969�j�B | |||
| �����ŁA����́A������̐��w�������������j����i�� | |||
| ���ȁ@���傢��1898 -1970�j�ɑ��k�����Ƃ���A���j�������u�O�����̒藝�v�Ɩ� | |||
| �������Ƃ̂��Ƃł��B | |||
| �@���̖��j����̐�U�́A���w��b�_�ł������A������c�N�w�ɂ����w���[���A�� | |||
| �c�N�w�̐��c�����Y�i�ɂ��� �������낤1870-1945�j���g�����������Ă����قǂł��B | |||
| ����A���쒼��������i�����������j���̗��h�Ȑ��w�̋���҂ŁA���݂܂� ���A | |||
| ���A���Z����ΏۂƂ������쒼���܂������Ă��܂��B���̏܂̊֘A�Ŗڂɕt�������� | |||
| �ɁA��6�́u��5���ł���킷�ɂ́H�v��A��2�́u�싅�̍œK�ŏ��̐��w�I�l�@�v | |||
| �Ȃǂ�����܂��B | |||
| �@�u�O�����̒藝�v�́A���c���݂Ă��A�g���̗]�n�����A�f���炵���������Ǝv�� | |||
| �܂��B�䂪�������łȂ����O���ɂ��L�߂������炢�ł��B | |||
| �R.�@�s�^�S���X�Ƃ��̌��ЂƖ������ɂ��� | |||
| �@�s�^�S���X�i��BC570 - BC500�j�́A30��̂��돔���𗷂��A���̂����ABC1000�N�� | |||
| �딭�B�����Ñ�o�r���j�A���w��Ñ�G�W�v�g���w�ɂӂ�A�O�����̒藝�ɊW���� | |||
| �u�s�^�S���X�̎O�g���i���p�O�p�`�ł��̎O�ӂ����R���̔���Ȃ��O�̑g���G�� | |||
| ���i3,4,5�j�Ƃ��i5,12, 13�j�Ƃ��i7,24, 25�j �j�Ȃǂ�m�����v�ƌ��������L�� | |||
| �ł��B������A�����s�^�S���X���A�u�O�����̒藝�v�������������������̂悤�ɐ� | |||
| �������̂��A�����A���̒藝���u�s�^�S���X�̒藝�ƌĂԂ悤�ɂȂ������R���v�Ƃ� | |||
| ������嗬���Ȃ��Ă��܂��B | |||
| �@�s�^�S���X��40�˂ɂȂ������A�͂��߂ď����ȋ��c��������̂ł����A�ނ̃J���X | |||
| �}������`���Ă��A�ǂ�ǂ�傫�Ȍ��Ђɐ����������悤�ł��B�����A���̌��Ђ� | |||
| �u�s�^�S���X�w�h�v�ƌĂԌ���������悤�ł����A���̂́A���̔閧���ЂŁA�ǂ� | |||
| �炩�ƌ����Ə@���F�̋������c�������悤�ł��B���̋��c���M�Ă������`����� | |||
| ���m���Ă��܂����A���̒��Ŏ��Ɏ������`�����w��傫�ȈӖ��������Ă��܂��B | |||
| �@�u�����Ƃ��Č����Ɍ������̂Ɍ����ċc�_���A�S�Ă̐��́A���R���̔�ŕ\���� | |||
| ��B�v | |||
| �@���̋��`�́A�����Ō����L�����݂̂𐔂ƔF�߁A�������������̐��E�ł͌���Ȃ� | |||
| �̂ŗe�F���Ȃ��ƌ������̂ł��B���������ۂɂ͒��p���͂��ޓ�ӂ��P�ƂQ�̎O�p�` | |||
| �̎Εӂ́A��5�@�̒����������A���݂��邪�A����������Ȃ镪���i�L�����j�ł��\�� | |||
| �Ȃ��̂ł��B���̋��`���s�^�S���X���Ђ̈�̌��_�������Ǝv���܂��B����Ɋ֘A | |||
| ���Ď��̗l�ȋL�^���c���Ă��܂��B | |||
| �@�s�^�S���X�̒�q�̈�l�A�q�b�p�\�X�iHippasus�j���D���Ŗ������������Ƃ��A | |||
| ��L���`�ɔ�����ƌ������ƂŁA���̒�q�������q�b�p�\�X��D�O�֓����̂āA�E�Q | |||
| �����Ƃ������Ƃł��B | |||
| �@�Ƃ���ŁA���݂܂Łu�O�����̒藝�̏ؖ��v���s�^�S���X����т��̒�q���s���� | |||
| �ƌ����L�^���݂����Ă��Ȃ������ł��B���c���v���ɂ́A�Ⴂ���ɒm�����Ǝv��� | |||
| ��O�g���̒��p�O�p�`�ł͖�肪�Ȃ��̂ł����A��� |
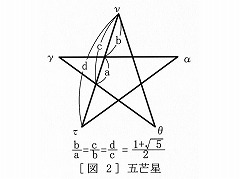
�}�Q_��䊐� |
||
| �̒��p�O�p�`�ŎO�����̒藝���������邱�Ƃ������ƁA | |||
| �K�R�I�ɖ����������Εӂ��o�����邱�ƂɂȂ�A���� | |||
| �̋��`�Ɩ�������̂ŁA�O���ɘR�k����̂�����A���� | |||
| �āA�ؖ����c���Ȃ������̂ł͂Ȃ����Ɛ��@���Ă���� | |||
| ���B���̌��Ђ͐}�Q���V���{���E�}�[�N�Ƃ��ċ��ɂ� | |||
| �g�S�g���Ɍ��N�ł���l�̏W�܂�h��\���Ă����悤�� | |||
| �����A��ρA����Ȃ��ƂɁA���̃}�[�N�̌�䊐��́A�� | |||
| ��̖������ł��鉩�������i1+��5�j/ 2�@�̂����܂�̂悤�Ȑ}�`�ł��i�}�Q�Q�Ɓj�B | |||
| �Ȃ��A���܊p�`�̍�}�@�����̌��Ђ������m���Ă����悤�ł��B | |||
| �@�ȏ�O�����̒藝�ƃs�^�S���X���Ђ̊W���q�ׂĂ��܂������A�S�Ȃ炸���ނ�� | |||
| ���_�������炤���ƂɂȂ��Ă��܂��܂����B���̂܂܂ł̓s�^�S���X�ɂ��āA�� | |||
| �����C���[�W�������ꂩ�˂܂���̂ŁA�O�����̒藝�Ƃ͖��W�ȕʂ̑��ʂ��O�G | |||
| �ꂳ���Ă��炢�܂��B | |||
| �@�s�^�S���X�́A1.8m���钷�g�Ɗ����ȓ��̂������Ă����Ƃ̋L�^������܂��B | |||
| �ނ�60�˂̂Ƃ��A���炭���E���̏������w�҂̃e�A�m�ƌ������A�V�l�̎q����ׂ��� | |||
| �Ƃ����L�����������Ȃ�A���l�I���̂̎����傾�����Ƃ݂č��x���Ȃ��ł��傤�B | |||
| �܂��A���_�I�Ȗʂł́A��ɉ��₩�Ŋ����\�ɏo�����A���t�������Ȍ��Ŋܒ~�ɕx | |||
| ��ł����Ƃ̂��Ƃł��B����Ƃ��A600�l���̒��O���ނ̉����ɏW�܂�A�����Ɋ������A | |||
| �ƒ���̂ĂĂ��̏�Ŕނ̌��Ђɑ������ƌ�����b���c���Ă��܂��B | |||
| �@�����A�s�^�S���X�̂悤�ȗ���̐l���A�u�m�ҁv�Ƃ��u���ҁv�Ƃ��Ă�ł����悤 | |||
| �ł����s�^�S���X�́A�����ǂ��Ƃ����A�����Ɂg�^�������悤�Ɠw�߂�l�h�� | |||
| �Ӗ�����u�N�w�ҁv�ɓ����錾�t���g�킹�Ă����悤�ł��B�����A��X���g���Ă��� | |||
| �u�N�w�v�̌ꌹ���A�����ɂ���Ƃ�������L�͂ł��B�܂��A�ނ̖v�㊈���Ñ�M | |||
| ���V���̖{�i�I�N�w�҃v���g���i�p�FPlaton BC427-BC347�j�ɂ����w�A���Ɋw�� | |||
| ����Ɨ։��]���i���˂Ă傤�j�̎v�z�ʼne����^�������悤�ł��B | |||
| �S.�@�e��ؖ��ɂ��� | |||
| �@���̒藝�̏ؖ��͐������ɂ���邪�A100����500�ʂ������Ƃ̂��Ƃł��B | |||
| �S�D�P�@���[�N���b�g�̏ؖ� | |||
| �@���̏ؖ��͗L���ȃ��[�N���b�h���́u���_�iBC300�N�j�v�ɂ̂��Ă�����̂ŁA���� | |||
| ����؋��̎c���Ă��钆�� |
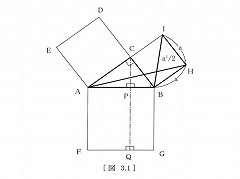
�}�R�D�P |
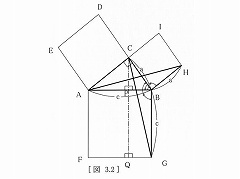
�}�R�D�Q |
|
| �ŌÂ̏ؖ��������ł��B�� | |||
| �̏ؖ��́A�������Ɋw | |||
| �҂��������ĒN�����m���� | |||
| ���鎟�̂Q���@�ƇA������ | |||
| ������g�p���A�قƂ�ǐ� | |||
| �����g�p���Ă��Ȃ��_�ɓ� | |||
| ��������܂��B | |||
| �@�@ ��ӂƍ����������O�p�`�́A�����ʐς����B | |||
| �@�A ��ӂƂ��̋��p�̓������O�p�`�͍����ł���B | |||
| �@�܂��A�}�R�D�P�́�BHI�Ɓ�BHA�́A�@�ɂ�蓯��a^2 /2�̖ʐς����B���ɁA | |||
| �}�R�D�Q�́�BHA�Ɓ�BCG�́A�A�ɂ��A�����ŋ���a^2 /2�̖ʐς����B | |||
| �i�����ǒ��F^2�@�͂Q��̂��Ƃł��B�j | |||
| �@���ɁA�}�R�D�R�́�BCG |
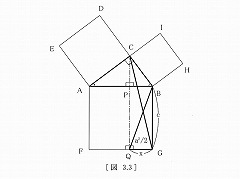
�}�R�D�R |
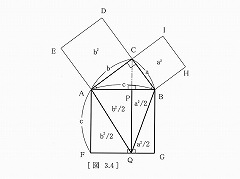
�}�R�D�S |
|
| �Ɓ�BQG�͇@�ɂ�蓯���� | |||
| ��a^2 /2�����B���l�ɁA | |||
| �}�R�D�S�́�BQP��a^2 /2 | |||
| �̖ʐς����̂Ł�BGQP�� | |||
| �ʐς́Aa^2�ł���B | |||
| �}�R�D�S�́�AFQP�̖ʐς� | |||
| ���l�ɂ�b^2�ł���B | |||
| ���������āA��ABGF�̖ʐ�c^2�͎����ŗ^������B�@a^2+b^2��c^2�@[�ؖ���] | |||
| �S.�Q �悭���ȏ����̗p���Ă���ؖ� | |||
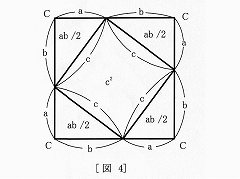
�}�S |
�@����͐}�S���g�p������̂ŁA�傫�Ȑ����`�̖ʐ� | ||
| �ia+b�j^2�́A���p�O�p�`�̖ʐρiab�j/2�̂S�{�Ə��� | |||
| �Ȑ����`�̖ʐ�c^2�Ƃ̘a�ł��邱�Ƃ��g���Ă��܂��B | |||
| �@�����F�ia+b�j^2��4 ab/2�@+ c^ 2 | |||
| �@���@a^2 + 2ab + b^2��2ab +c^2 | |||
| �@�� a^2�@+ b^2��c^2�@�@�@[�ؖ���] | |||
| �S.�R�@���c�ƃA�C���V���^�C���̏ؖ� | |||
| �@�������̒藝���K�����̂��@��ɁA���̒��ōł��V���v���Ȑ}�ŏؖ����悤�Ǝv�� | |||
| �����A�l�������̂��}�T�ł��B���Ȃ݂ɉ��c��84�˂� |
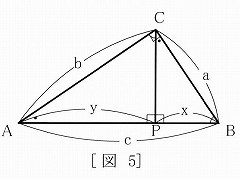
�}�T |
||
| ���ł����B���̏ؖ��́A���̇@�ƇA���g�p���Ă��܂��B | |||
| ���p�����_C����ΐ�AB���������낵�����̑���P�� | |||
| ���A�}�T�̂悤��x��y���`���܂��B | |||
| �@�@ ���̌��ʂł���O�̎O�p�`�́A�݂��ɑ����ł��� | |||
| �@�@�i����p���������̂Łj�B | |||
| �@�A AB�̒���c�́ix+y�j�ł���i��x, y�̒�`���j�B | |||
| �@[�ؖ� �J�n] | |||
| �@�@ ���A��ABC�Ɓ�BCP�ԂŎ�������������B | |||
| �@�@a/c�@�� x/a�@�@,�@�@��a^2�@��cx�@�i�� a, c ���@0 �j�B | |||
| �@�@ ���A��ABC�Ɓ�CAP�ԂŁA��������������B | |||
| �@�@b/c�@��y/b�@�@,�@�@���@b^2�@��cy�@�i�� b, c ���@0 �j�B | |||
| �@��L��̎��̘a���Ƃ�ƁA������B | |||
| �@�@a^2�@+b^ 2��c�ix+y�j | |||
| �@���̎��́ix+y�j�́A�A�ɂ��c�Ȃ̂ŁA������B | |||
| �@�@a^2 +b^2��c^2�@�@�@�@�@�@�@[�ؖ���]�@�@�@�@ | |||
| �@���̏ؖ����������Ă���A�����}���g���Ă���l�����邩���E�E�E�Ǝv���A���ׂ� | |||
| �Ƃ���A�����̐�l�����̐}���g���Ă��܂����B���̂Ƃ��A���ΐ����_�ŗL���ȃA�� | |||
| �x���g�E�A�C���V���^�C���i�ƁFAlbert Einstein�@1879-1955)�i���P�j�����N�̍� | |||
| �i���Q�j�ɁA���̐}���g���ĎO�����̒藝���ؖ����Ă������Ƃ�m��܂����B | |||
| �@�A���x���g�V��́A���c�Ɠ��l�A�O�L�@���g�p���Ă��܂��������c�̇A�̂����ɁA | |||
| �����ŏo������ACP�Ɓ�BCP�̖ʐς̘a�����Ƃ́�ABC�̖ʐςƓ��������Ƃ��g�p������ | |||
| ���ł��B����́A���c��x + y = c�Ǝ��͓����ł����A�ؖ�����╡�G�ɂ��Ă��܂��B | |||
| ��̓I�ɃA���x���g�V��̂�����ؖ������c���Ă��Ȃ������ł����A�O�p�`�̖ʐϊ� | |||
| �W���g�p����ɂ́A���̓�ʂ�̕��@���l�����܂��B | |||
| �@�B ���p�O�p�`�̖ʐς����߂�������g�p����B | |||
| �@�C�@�����`�̖ʐϔ䂪������̓��ł���B | |||
| �@������ɂ���A��ǓI�ɂ݂�Ƃ����́A����̏ؖ��Ƃ݂�ׂ��ł��傤�B | |||
| �@�i���P�j�ނ̒a�����R��14���́g�̓��h�ł��B���{�ł́g���w�̓��h�ł��B | |||
| �@�i���Q�j�W�ˁA11�ˁA12�˂̎O�̐�������܂��B | |||
| �T.�@�u�l�����̒藝�v�Ɓu�l�g���v | |||
| �@���̎O�����̒藝�ɂ͊g���̗]�n�����X����܂��B���ɒ��ڂ��Ċg�����邩�ɂ�� | |||
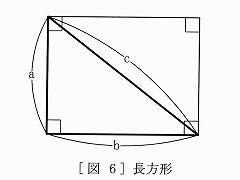
�}�U |
�āA�S�����e�������܂��B | ||
| �@�����ł́A�ΏۂƂ���}�`�̒��鎟����������グ | |||
| �邱�Ƃɂ��܂��B�O�����̒藝���ΏۂƂ���}�`�́A�� | |||
| �ʁi���j���̒����`�ł���A���̓��̕ӂƑΊp�� | |||
| �̊W���������藝�Ƃ݂邱�Ƃ��ł��܂��i�}�U�Q�Ɓj�B | |||
| �����Ō����u�l�����̒藝�v�Ƃ́A���́i�O�����j���� | |||
| �����́i�}�V�Q�Ɓj��ΏۂƂ��āA���̎O��̕ӂƁi��j | |||
| �Ίp���̊W��\�������Ƃ��܂��B�i�}�V�Q�Ɓj | |||
| �@a^2�@+b^2 + c^2�@�� d^2�@�F�u�l�����̒藝�v |
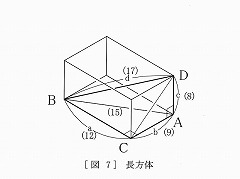
�}�V |
||
| ���̌����́A�O�����̒藝���x�g�p���邱�Ƃɂ��A | |||
| ���o�ł��܂��B | |||
| ��ABC�ɂ����� | |||
| �uAB�v ^2��a^2 + b^2�@�i�� �O�����̒藝 �j | |||
| �i�����ǒ��F����AB���uAB�v�ŕ\���܂��B�j | |||
| ��BAD�ɂ����� | |||
| �uBD�v^2�@���uAB�v^2�@+�uAD�v^2�i�� �O�����̒藝 �j | |||
| �@���@d^2 �� a^2 +b^2 + c^2�@�@�@�@�@[�ؖ���] | |||
| �@���A�Z��̘a�����l����ƁA�i���āA�悱�A�������j�F���ia, b, c�j�Ƃ����ƁA | |||
| �ia, b, c�j���i12��,9��,8�ځj�ɂȂ�܂��B�����}�V�ɕt�L���Ă����܂����B | |||
| ���̕����̍Œ��Ίp���i��Ίp���jd�́A�Fd^2��12^2+9^2+8^2�� 289�i��^2�j | |||
| ���@d����289�@��17�i�ځj�@�@�i��@d > 0�@�j �ƂȂ�A���傤��17�ڂɂȂ�܂��B | |||
| ���������āA�i12,�@9,�@8,�@17�j�́A�u�s�^�S���X�̎l�g���v�ƌĂԂׂ��g���ł��B | |||
| ������u�s�^�S���X�̎O�g���v | |||
| ��g�F�i 12,�@9,�@15�j | |||
| �@�@�@�@�@�@�@�@�@ll�@�@�@�@�@�@�@�@�ˁ@�@�@�@�i12,�@9,�@8,�@17�j | |||
| �@�@�@�@�@�@�@�@�i15,�@8,�@17�j | |||
| ���狁�߂��܂��B | |||
| �@�ȏ�Ɏ������悤�ɁA�u�l�����̒藝�v�́u�O�����̒藝�v���x�A�u�s�^�S���X | |||
| �̎l�g���v�́A�u�s�^�S���X�̎O�g���v��g���狁�܂�̂ŁA���قǏd�v�Ȓ藝 | |||
| ��g���ƔF�߂��Ȃ����߂��A�u�l�����̒藝�v���u�s�^�S���X�̎l�g���v������ | |||
| �܂ł��̕���Œ蒅���Ă��܂���B�O�̂��߂ɁE�E�E�B | |||
| �U.�@������ | |||
| �@����A�L�u�̕��ɒ����E���� �肢�����������L���Ă����܂��B | |||
| �U.�P�@�O�����̒藝�̃E���̏ؖ��B�����A�u�O��a,b,c��a^2+ b^2��c^2�@���� | |||
| �@�@�@�Ƃ��A���̎O�p�`�͒��p�O�p�`�ł���v�̏ؖ��B���ɁA�I���e�����u���p�O�p | |||
| �@�@�@�`�Ȃ�@a^2+ b^2��c^2�@����������v���g�p���Ȃ��ؖ����]�܂�܂��B | |||
| �U.�Q�@a^n+b^n��c^n�@,�in��{3�ȏ�̎��R��}�j���������邩�H | |||
| �U.�R�@z1,z2�����f���ɂ����āA|z1|^2 + |z2|^2��|z1+z2|^2�@���������邽�� | |||
| �@�@�@�̏����́H | |||
| �U.�S�@��2 ���i�L�����j�ŕ\���Ȃ����Ƃ̏ؖ��B | |||
| �U.�T�@�s�^�S���X�̎O�g�����o�͂���v���O�����H | |||
| �@�{�����ܘb�ɁA�s�s���ȓ_�����X���邩�Ǝv���܂��B���C�t���̕��́A���c���� | |||
| �A�����������B�@ | |||
| 2017. 6.25 | ���� | ���������{�w�I�s�ƃG�b�Z�C�œǂލ�Ƃ̎R���x��ǂ� |  |
| ���������{�w�I�s�ƃG�b�Z�C�œǂލ�Ƃ̎R���x��ǂށ@�@�@�@ | |||
| ���l�s�@�����@�L�� | ||
| �P�D�͂��߂� | |||
| �@�������珺�a�ɂ����Ă̓��{�̍��48�l�̎R�Ɋւ���I�s���Ȃǂ�Z�߂��w�I�s�� | |||
| �G�b�Z�C�œǂލ�Ƃ̎R���x�Ƒ肷�镶�ɂ��R�ƌk�J�Ђ̕ҏW�ɂ���ă��}�P�C���� | |||
| ���獡�N�i2017�j�R���P���ɏo���ꂽ�B�[�c�v���V�c���Y�̂悤�ɎR��������I�s | |||
| �̑�ނɂ����ƂȂ�Ƃ������A��Ƃ�̐l�A�o�l�A�]�_�ƂȂǂ��R��R���������L | |||
| �������͂�Z�߂����̂͑������߂Ă̎��݂ł͂Ȃ��낤���B���҂����߂đ������߁A | |||
| ������薡����ēǂB���Ɉ�ۂɎc�������12�l�̍�i�ɂ��āA�ȉ������Љ� | |||
| �������B | |||
| �Q�D�S�Ɏc����12�l�̍�Ƃ��� | |||
| �P�j���_�@�w�x�m�R�i���j�x | |||
| �@���N�������ɕҏW����Ă��邽�߁A���_�����Ԗڂɓo�ꂵ�Ă���B�̗p���� | |||
| ���w�x�m�R�x�̏�����������O�Y�̖ōڂ��Ă���B�A�����Ă܂����܂�Ԃ��Ȃ� | |||
| �����̂��A�����̖��̕t�����n���������������ƌ����āA�����ɕ��͂ɂ��̋C������ | |||
| �\�����B | |||
| �@�u���͂܂��܂��ʉ��ŁA�܂��܂��������B�������͐� |

��Ƃ̎R�� |
||
| �X�����i�قӂ��j���˂Ν����オ��Ȃ������B�֖�̂� | |||
| ���ȏꏊ�ł́A��q�̏������S�i���j���ēo�����B�� | |||
| �͌��ȂǂƂ��������̖��̕t�������낵���ꏊ���������B | |||
| �\�\�����̗����̊G�ɂ���A�q���̖S�삪�ςݏグ��� | |||
| �̂悤�ɁA�ςݏd�Ȃ����₪�U����āA��ʉ��F���� | |||
| ���āA�r��������i�v�B | |||
| �@�x�m�̎R������̒��߂����тƂ��āA����ۂ�f | |||
| ���Ɏ��̂悤�ɕ\�����Ă���B���Ɋ����ł���Ȃ�����e���Z���Ɗ��������� | |||
| �@�u���������̌i�F�A�S���i�}�C���j�����n�����̒��߁A���������Ȗ��̂悤�Ȑ��E | |||
| �̌��A��E�̔@�������A�������茞��������_�̕s�v�c�Ȍ`��\�\���ׂĂ��̌��i�́A | |||
| �܂����̌��i�������A���̍��܂�Ƌ�ɂ��Ԃ߂Ă����\�\�����Ƒ����o�������̏� | |||
| ��B���A��ԍ�����ɏ���Ċ�𓌓V�Ɍ����A�s��ȑ��z��q��ŁA�_���̋F���� | |||
| ������Ă���\�\���̙��߂̈̑�Ȃ鎍���́A���̐S���ɓO�����B��O�̂��̑� | |||
| ���Ȍ��i�͍ő������ׂ��炴��L���ƂȂ����̂ł���B���̒q�͂͏��ł���͓y�ɉ� | |||
| ���Ďd�����Ă���A���̐��܂�Ȃ����������́A���x�m�̐Ⓒ���爮���߂� | |||
| �����̐l�X�̊�̓y�������̂ƁA�������鎞�܂ŁA���̋L���̈�X���ׂȓ_�͏��ł� | |||
| �邱�Ƃ͂Ȃ��v�B | |||
| �Q�j�^�Ӗ쏻�q�@�w�����֓����S�x | |||
| �@���{�e�n�֗����A�����̉̂��r�^�Ӗ쏻�q�����a�V�N�ɕ\���������w�����֓� | |||
| ���S�x���M�҂ɂ͂��̕��ɂ̕ҏW���\���镶�ɈႢ�Ȃ��Ǝv�����B | |||
| �@�o�����̕��u�l�Ԃ͑��n�ɏZ��ł���B����œV�Ƃ��R�Ƃ������ō����Ƃ� | |||
| ��֓����S���A�I�v�ȑ�̖̂�ؐl�����Ɏ����Ă���B�������ɍ݂���̂͑��z�� | |||
| ���A�_�ł��A����ł����ׂĔ��������̂Ɋ�������B����������łȂ��A�C�� | |||
| �����́A�̂����́A�_��Ȃ��̂ɂ�����������B�_���V�ɏZ��Ől�Ԃ��i�z����� | |||
| �l���ď@�������������̂��A���Ƃ͍��̍����ɓ����S����ł������B�i�����j�G�� | |||
| ���R�x��]��ʼnĊ��ɓo�R�~��������ꂽ�肷��̂́A��߂Ȃ��̂����A�䂪�g�� | |||
| �����u���v���C�����̂����̂Ƃ��Ċ������邩��ł���B�v�́A���{�l�̑f���ȐS | |||
| ���f���o���Ă��āA���قǂ́u�Ċ��ɓo�R����l�X�́A����[�i���j��A��������� | |||
| �ړI�̐l������B�A���̏W�̐l������B�n���̒T���A�C�ۂ̌������u���l������B�� | |||
| �����̂悤�ɉ̂��r�ނ̂�ړI�Ƃ���l������A�܂������̐l�̗e�Ղɓ��܂Ȃ����� | |||
| ���Ղ��ėD�z���������悤�Ƃ���l������B�v���傢�ɋ����ł���B | |||
| �@�M�҂����ۂɌi�F���G�M�ɑ�������A���������Ԃ⒱���J�����Ɏ��߁A�V�����ʂ� | |||
| ���R����n�}�ɈȂǎR�o���傢�Ɋ��p���āA���낢��̎�������i�� | |||
| ���Ă������Ƃ����X�̂悤�Ɏ���������ꂽ�B�܂��A�I���̒��߂�����̕����悢�B | |||
| �u�R����A��S�͏�߂��Ă���B�����Z������ł���B���̐������₩�ɂȂ��� | |||
| �S�������āA�V�����n��̐����ɎQ������������B�i�����j�����R�֍s���S���́A�� | |||
| �ł��V�̈ꕔ�ֈ����グ��������ł���B�v�M�҂�����̎R�s��̐S����� | |||
| �u�₩�����v���o�����B | |||
| �R�j�J�菁��Y�@�w���̂��낢��x | |||
| �@�w���̂��낢��x�i���a58�N�j�̒��ŁA���܂�ɕ֗��ɂȂ��ē��{�̉��n�܂ŊJ�� | |||
| ����āA�s�����čs���p�Ɍx����炳��Ă���ȉ��̕��͂ɑ傢�ɋ������B | |||
| �@�u�����čג������y�̏�֏c���ɓS���Ԃ��~����āA���ꂪ�N�X�A���ǂ̐悪 | |||
| ��ɂ����čs���悤�ɋ��X�ւ܂ŐL�тčs���āA���y�����]���Ȃ���Ԃł����� | |||
| �݂�A�D�J�̉��̕������Ȃ��R�ԗH�J�͈̔͂Ɖ]�����͎̂���ɂ����߂���� | |||
| ��ł���B�����֎����ė��āA�S���ȁA�ό��ǁA�c�[���X�g�E�r���[���[������̐� | |||
| �`�@�ւ������ڂȂ��q��U�����邩��A�����Ƃ����������F���̓y�n�̓��F�������A | |||
| �s��̉����ɂȂ��čs���B���͎R�o��͌����ł��邩����{�A���v�X�̔ɏ�����l�q | |||
| ���������Ƃ͂Ȃ����A�����R�̗ǂ��Ɖ]�����̂́A�l�E�z�����Y��Ȋ����A�l�� | |||
| �Ɉ˂��ĉ����ꂴ�鐴����C���ċz����_�ɂ���̂ł͂Ȃ����B�Ðl�̖������ҍ��� | |||
| ��Ɖ]���A�V�n�̗I�v�����Ɖ]���A�_�升��̋��ɗV�ԂƉ]���̂��A�R�o��̎ | |||
| �Ȃ̂ł͂Ȃ����B���������ł���Ȃ�A�����̐M�z�n���̂悤�ɐ�`����Ă��܂��� | |||
| �̂ł́A�R�x�Ƃ��Ă̈Ӌ`��������ł���B�v | |||
| �S�j�����Y�@�w�R�ɓo��x�i�吳�U�N�j | |||
| �@�u�R�ɓo��@�@�\����肠�鏗�ɑ���[ | |||
| �@�@�R�̒���ɂ��ꂢ�ȑ��ނ炪����A���̏�ł킽�������͐Q�]��ŋ��� | |||
| �@�@�ڂ������ĂƂق��[�̕��߂�ƁA�����߂�ɂЂ�т�Ƃ����C�̌i�F�̂₤ | |||
| �@�@�ɂ����͂ꂽ�B | |||
| �@�@ | |||
| �@�@��ɂ͕����Ȃ���Ă���A����͏����Ђ���Č��ɂ��ĂȂ���A | |||
| �@�@�ǂ��Ƃ������Ă��Ȃ��ɁA�ڂ��ڂ��Ƃ����R�̒�������邢�Ă�B | |||
| �@�@����͂��܂ł��A���O�̂��Ƃ��v���Ă��̂ł���v�B | |||
| �T�j�F��_��@�w���ꂩ�炻��x�|���֎R�x���f�Ёi���a�X�N�j | |||
| �@�F��_����͂��߂Ƃ��āA�����̖������R�ɂ��Ă̕����Ă��邪�A�F��l�� | |||
| �����G���́w���{�A���v�X�x�A�w���{�R���_�x�A�u��d�V�́w���{���i�_�x�����菊 | |||
| �ɂ��Ė��������p����Ă��āA�R�Ɋւ�����{�̌ÓT�����Ȃ肵�����肵�����̂��� | |||
| ���Ă��邱�Ƃ����߂Ď��������B | |||
| �U�j�����H�N�q�@�w�c��x�i���a36�N�j | |||
| �@�����H�N�q���\�����w�c��x�Ƒ肷��o��ƋI�s���ŒԂ������{����̌㗧�R���� | |||
| �Ɣ��Α��̔������i�����ɂ͔������̕����͈�،����Ȃ����j�ւ̕����A��r�I�ɍ� | |||
| �߂̂��Ƃ�\���Ă���̂Əo�ł��ꂽ�N���M�҂������v��ɓ��Ђ����N�A���a36�i19 | |||
| 61�j�N�ł��������ߓ��ɒ��ӂ��ēǂB | |||
| �V�j���鈣���ʁ@�w�����R�ق��x�i���a11�`27�N�j | |||
| �@�A�����M�̑I�҂̈�l�ł��������鈣���ʁi�䂤���E�����������j�o����26�i1893�j | |||
| �`���a49�i1974�j�N�p�������R�A���C�R�A���B���ǘA��A�����A��A�іL�R��A���� | |||
| �x�E�����A���r��R��ǂ̂��M�҂��قɔ������R�i�������Ԏv�������Ċy������ | |||
| ���B | |||
| �W�j�啧���Y�@�w�R�Ǝ��x�i���a30�N�j | |||
| �@�啧���Y�����a30�i1955�j�N�Ɂw�R�ƌk�J�x���ɔ��\�����w�R�Ǝ��x�Ƒ肷�镶�� | |||
| �������ɗF�l�ɎR�������āA���̉e���������A�܂��A�����̑�\��w���H�x���� | |||
| ���j�̖؊x��ɓW�J���ꂽ�w�i��璆�w���̍��ɓ��{�A���v�X�J��̕��v�E�E�G | |||
| �X�g���i1861�`1940�N�j�̍u�����_�c�̖^���ŏ����G���̒ʖ�ŕ������b�Ƃ��M�� | |||
| �����߂Ēm�������Ƃ���������ԗ�����Ă��āA�����ÁX�œǂB | |||
| �X�j�䕚����@�w�V�h�x�i���a�U�N�j | |||
| �@�䕚������B�҂Ȑ��M�^�b�`�ő����̎R�̑̌���Ԃ�A�[�c�v���ʂ��ĎR������ | |||
| ��ꂽ�����Ԃ��������w�V�h�x���傢�ɎQ�l�ɂȂ����B�����Ɗ������邱�Ǝ��� | |||
| �ł������B | |||
| 10�j��[�N���@�w�_�Öq��s�x�i���a11�N�j | |||
| �@�����w�_�Öq��s�x�͐_�Öq��o�c�҂̉Ƒ��̐l���`�ʂ���͂̎��R�`�ʂ������� | |||
| ���˂̎�����̍�i���Ƌ����Ɏ������Q�����肾�����B | |||
| 11�j�ҁ@�M���@�w�_�ɂ����Ԃ����䍂�x�i���a61�N�j | |||
| �@�������{���Z�ɓ����Đ[�c�v��̎R�̖{��E�C���p�[�́w�A���v�X�o���L�x�Ȃǂ� | |||
| �h������ĎR���ɐe���ҁ@�M���̎��̕��͎͂R�j�̐_����˂��Ă���B | |||
| �@�u�R�j�Ƃ����̂́A�����ŁA���}���I�ŁA�ǖقŁA�� |

���s�ԓ` |
||
| �Ƃ��D�ސl�������B���{�ȗ��O��̃O�����f�����@���g | |||
| �ɍs���ăA�C�K�[�k�ǂ����グ���Ƃ��A�R�ɂ͋���̕\ | |||
| ����邱�Ƃ�m�����B���̋������������̂́A���� | |||
| �E�C�ƈӎu�̗͂������B�v | |||
| �@�����̕����V�N�ɐV���Ђ��犧�s���ꂽ�w���s�ԓ`�x | |||
| �͒J�菁��Y�܂������҂ŁA�����̔�]�Ƃ���ҁ@ | |||
| �M���́w�ԓ`���x�Ɖ]���ׂ��Ƃ̕]�Ă���B�Y��� | |||
| ���͂Ɠ��{�e�n�̐��s�̗V�s�̐Ղ��A���̂Ƃ��ǂ��ɉr�܂ꂽ�̂�D������ĒԂ��A | |||
| �������M�҂̗��̃o�C�u���̈���Ƃ��ĕ��ɔł����E�ɉ�����ǂݕԂ��Ă���B | |||
| 12�j�k�@�m�v�@�w�R�o��̂��Ɓx�i���a40�N�j | |||
| �@�R�D���͋����ď��{���Z��_���Ėҕׂ��d�˂����A�k�@�m�v�����̈�l�ŁA������ | |||
| �a�����ăq�}�����o�R�����ɂ��Ȃ��Ă���B�����͑��l���m�钎�D���i�w�h�N�g���} | |||
| ���{�E�����L�x�̒�������j�ŁA���̂��ߒ������߂ĉ��������������K�˂����Ƃ� | |||
| ������Ă��邵�A�g���������[�h�̏Љ������Ă���B | |||
| �R�D������ | |||
| �@���͂������Ď�ɂ���������������A���҈ȏ�ɖʔ��������B�ȏ�����钘���� | |||
| �Ƃ̒�����S�̂̎l���̈�̍�Ƃ������グ���Ȃ��������A�������A���̃��j�[ | |||
| �N�ȕ��ɂ̑_���₻�̓��e�̗֊s�͗������Ă����������̂ł͂Ȃ����Ǝv���Ă���B | |||
| ���̂g�o�ǎ҂̊F�l�ɂ�����ɂ������Ĉ�ǂ���������Ǝv������ł���B | |||
| �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�� | |||
| �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@2017�N�S���P���i�y�j�@�@�L | |||
| 2017. 6. 8 | ���� | �ʔ����ǂw���E�V�ˋI�s�x |  |
| �ʔ����ǂw���E�V�ˋI�s�x | ���l�s�@�@���� �L�� | |
| �@���̖{�̓j���[���[�N�E�^�C���X�̋L�҂�S�Č��������iNPR�j�̓��h���Ƃ��ăj | |||
| ���[�f���[�A�G���T��������ѓ����ɕ�炵�����Ƃ̂���G���b�N�E���C�i�[�iEric�@ | |||
| Weiner�j��2016�N�ɕ\�����gThe Geography of Genius, A Search for the World�fs | |||
| Most Creative Places from Ancient Athens to Silicon Valley�h�@�̖�{�ŁA440�� | |||
| �����ł���B | |||
| �@�u�^�̓V�ˁv�ɂ͏C����͕t���Ȃ��ƒ��҂̃��C�i�[ |

���E�V�ˋI�s |
||
| �͉]���B�Ⴆ�A�C���V���^�C�����u�Ȋw�V�ˁv�ƌĂ� | |||
| ����A���[�c�A���g���u���y�̓V�ˁv�ƌĂ�͂��� | |||
| ���B�V�˂͐�啪��������݂ł���A�ƁB�܂��A�� | |||
| ������������Ă������B����̐l���V�˂ł��邩�A�Ȃ� | |||
| ���̔��f��͉��Ȃ̂ł��낤���B���C�i�[�ɂ��A | |||
| �������A���̒��̑����̐l�X�������F�߂邱�ƁA���Ȃ� | |||
| ���Љ�I�]���Ȃ̂��ƌ����i�{����W�̓V���R���o���[ | |||
| �o.182�`183�j�B | |||
| �@���j��U��Ԃ�ƁA�V�˂����̓����_���Ɍ����̂ł͂Ȃ��A����̎����ꏊ�� | |||
| �W�����Č����X�������邱�Ƃ��킩��B�ނ�͂�������A�قړ������ɓ����ꏊ�� | |||
| ���݂��Ă����B�I���O400�N�O��̌Ñ�A�e�i�C�ɁA�\�N���e�X�A�v���h�A�A���X�g�e | |||
| ���X�A�g�D�L���f�B�f�X���B1500�N�̃t�B�����c�F�ɂ́A���I�i���h�E�_�E���B���`�A | |||
| �~�P�����W�F���E�u�I�i���[�e�B�A�{�b�e�B�`�F�������A1800�N����̃E�C�[�� | |||
| �ł́A�x�[�g�[���F���A�n�C�h���A�V���[�x���g�A�����Ă���ɂ̓��[�c�A���g���� | |||
| �Ȃɗ��ł����B�g�[�}�X�E�G�W�\���̂悤�ɁA���Ȃ��Ƃ��ꖜ���Ԉȏ�̓w�͂̌� | |||
| �ʂƂ��āA�u�V�ˁv�́u����ꂽ�v�B�������́A�V�˂́u�i�����y�n�Ɂj��� | |||
| ����v�ƁB�����āu�V�ˁv�͌����Ĉ�`�ɂ����̂ł͂Ȃ��ƒ��҂��f�����Ă��� | |||
| �̂��ȑO�ɁgGRIT�h���Љ�ĉ��Ă̌��݂̍l��������������悤�ɁA�̐l�͖{�l�� | |||
| �₦����w�͂Ǝ��s����̌��ʐ��܂����̂��Ƃ���l�����ɂ������ɕ�������ƕM | |||
| �҂͊����������B�@ | |||
| �@�M���V�A�̃A�e�l�i�N�w�j�A�����̍Y�B�i�Ȋw�̊�b�Ƒh�����ɑ�\����铂���j�A | |||
| �C�^���A�̃t�B�����c�F�i�G��A�|�p�j�A�X�R�b�g�����h�̃G�f�B���o���i��w�A�� | |||
| �w�j�A�C���h�̃J���J�b�^�i�^�S�[�����̃x���K���E���l�b�T���X�j�A�I�[�X�g���A | |||
| �̃E�C�[���i�Q��A���y�ƃt���C�g�ɑ�\����鐸�_�Ȋw�j�A�����čŌ�ɃA�����J | |||
| ���O���̃V���R���o���[�i�X�e�B�[�u�E�W���u�X���̖��̍Ő�[�f�B�W�^���Z�p�j�� | |||
| ����ꏊ�W�������V�˂���Ƃ��āA�Y������l�����L���A�������Ă���B���� | |||
| �ہA�����̗��j�����s��A���Ȃ킿�C���O�����h�̃����h���A�t�����X�̃p���A�h | |||
| �C�c�̃t�����N�t���g�A�{����h���X�f���A�C�^���A�̃��[�}�A�A�����J���O���̃j | |||
| ���[���[�N�A�t�B���f���t�B�A��{�X�g�������V�˂�����_�Ƃ��ċ����Ă��\�� | |||
| �ɑΏۂƂȂ�V�˂�����ƕM�҂ɂ͎v���邪�A������Ă��Ȃ��̂����̂��A�t�ɋ� | |||
| ����U�����B�������܂�ɂ��G���Ȑl�X��������藧�����苏�Z���đ��������� | |||
| �Ă��邽�߂ɂ�����荘�������t���ďW�������Ƃɓ���܂Ȃ��̂�������Ȃ��B | |||
| �@�V�˂͈�l�ł͂Ȃ��A�����悤�ȕ���ɕ����̋�������Ƃ������A�����悤�ȍˊo | |||
| �̎����傪����������������o���オ�邱�Ƃ�����ƌ��Ă���悤�ł���B | |||
| �@�M�҂���ϖʔ������҂̌��_���Ǝv�������Ƃ́A�w�V�˂n�̉�������͒� | |||
| �������Ȃ��A���\�N���A�������������I�قǑ����ƁA���̎n�܂�Ɠ����ɁA�˔@�Ƃ� | |||
| �ďI�����}����B�o���オ�����������͂邩�ɊȒP�ɕ���B���̌��_���炷�� | |||
| �ƁA���݂̃V���R���o���[�͊��Ɉꐢ�I�ȏ���V�˂̒n�Ƃ��ČN�Ղ��Ă���B������ | |||
| ���n���E�b�h�������A�A�����J���O���̂ǂ̓s�s�����������̒n�ʂ�ێ����Ă� | |||
| ��Ǝv���iP.420�j�x | |||
| �@���҃��C�i�[�́A�O���gThe Geography of Bliss�h�i�M��u���E�����킹�I�s�v�� | |||
| �S�ăx�X�g�E�Z���[�ƂȂ��ĉX�������d�ɓo�ꂵ���B���]�ԂƓ��{�̊������i���� | |||
| ��Ȃ�������l�ł�����Ƃ̂��Ƃł���B�V�˂��V�˂���y�n�Ƌ��ɔɉh���邽 | |||
| �߂̕K�v�\�������Ƃ��āA���҂̌��_�Ƃ��v����ȉ��̕��͂��M�҂ɂ͂������肵 | |||
| ���nj㊴�������炵�Ă��ꂽ�B | |||
| �@�w����������S�点����̂��A�K����������������p��������Ƃ͌���Ȃ��B���l | |||
| �͑n�ӍH�v�����āA�r���ŔR�����ւ��悤�Ƃ���B���l�b�T���X�̖u���́A�Ñ� | |||
| ���Y�̍ĕ]���ɒ[���邪�A�Ñ�̕��������������̐l����`�҂����́A���� | |||
| ���������̓Ǝ��̊T�O��n��A�m�I�������L�߂��B�V���R���o���[�����̂܂ܔɉh�� | |||
| ���������̂Ȃ�A����܂łƂ͕ʂ̃G�l���M�[�������t����K�v������B�܂�A�P | |||
| �ɑn���͂ɂ��ӂ��V���i�\����̂ł͂Ȃ��A�n���I�ł��邽�߂̐V���ȕ��@�� | |||
| ���t���Ȃ���Ȃ�Ȃ��iP.422�j�x�B | |||
| �Ƃɂ����ꕗ�ς�����ѐF�̈Ⴄ�����ȗ��s�L�ł������B�@�@�@�@�@�@�@�@�@�@�@���@ | |||
| �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@2017�N�R��11���i�y�j�@�@�L | |||
| 2017. 6. 2 | ���c | �@���U���Ă��A�Ԑ���I2017�N��: ���̂T |  |
| �@���U���Ă��A�Ԑ���I2017�N��: ���̂T | ���l�s�@�@���c�@�� �@ | |
| �@�@���U���Ă��A�u�S���s�s�Ή��悱�͂܃t�F�A�v�J�ÂʼnԁI�ԁI�Ԑ���I | |||
| �@�y�R�������z���E�E�E�E�@���@������L��E�E�E�݂ȂƂ܂����i�� | |||
| �@�R�������̎Ő����A���� |

�K�[�f���x�A�\�ƔU |

�ʐ^�X�|�b�g�X��� |
|
| �ꂽ�L�ꂩ��́A�g���ꂼ | |||
| �݂ȂƉ��l�h�Ǝv���� | |||
| ���i���ڂɔ�э���ł��� | |||
| ���B | |||
| �@����i�T/19)���K���Ȃ� | |||
| �ƂɁA���l���`�Ƃ��� | |||
| �u�U�v�ɏo����Ƃ� | |||
| �o���܂����B�ό��q�̊F����ɂ́A�V��̗ǂ��Ƌ��ɍō��̑��蕨�ƂȂ������Ƃł� | |||
| �傤�B�ܘ_�A���ɂƂ��Ă��ǂ���ނ��E�E�E�Ƒ��тł����B | |||

�}�����^���[ |

�����ƃ}�����^���[ |

�U�����߂�Ԃ��C�̏��̎q |
|

�U |

�L��̉�_�P |

�L��̉�_�Q |

�L��̉�_�R |

�L��̉�_�S |

�L��̉�_�T |

�L��̉�_�U |

�L��̉�_�V |

�L��̉�_�W |
| ���@�����̃o�����`�`�`190�i��E2,600���̃o���̋��� | |||
| �@�R���������́u�o�����v�́A�ʏ���t�E�H�Ɏs������ |

�u�o�����v_�P |
||
| ���ߑ����̊ό��q�̊F����̖ڂ��y���܂��Ă���Ă��� | |||
| ���B | |||
| �@�u�o���v�͕������N(1989�N)�X���A���l�s��100���N�A | |||
| ���l�J�`130���N���L�O�Ƃ��āA�u�s�̉ԁv�ɐ��肳��� | |||
| �����B | |||
| �@�@ | |||
| �@ | |||

�u�o�����v_�Q |

�u�o�����v_�R |

�u�o�����v_�S |

�u�o�����v_�T |

�u�o�����v_�U |

�u�o�����v_�V |

�u�o�����v_�W |

�u�o�����v_�X |

�u�o�����v_10 |

�u�o�����v_11 |

�u�o�����v_12 |

�u�o�����v_13 |

�u�o�����v_14 |

�u�o�����v_15 |

�u�o�����v_16 |

�u�o�����v_17 |

�u�o�����v_18 |

�u�o�����v_19 |

�u�o�����v_20 |

�u�o�����v_21 |

�u�o�����v_22 |
| �@�@�@�@�@�@�@�@�@�@�@ �y�ۂ̕@�p�[�N�z��� | |||
| �@ �y�ۂ̕@�p�[�N�z���Ƀ`���b�g��������o���܂����B�V���{���K�[�f���� �u�K | |||
| �[�f���x�A�[�̒�v�́A�V�����Ԃ�A���ς��A�V���Ȕ������Ŗڂ��y���܂��Ă���� | |||
| ���܂����B | |||
| �@����A��i�Ɩڗ������̂���ƁE�c�̏o�W�́u���ĂȂ��̒�v�Łu���܁v����܂� | |||
| ���i���j�T�J�^�̃^�l�o�W��i���V�����Ԃɓ���ւ��āA�ʐ^�̂悤�Ɍ����ȉ₩ | |||
| ���������Ă��܂����B���ꂪ�R������������u���܁v��������Ə�̏܂���܂����� | |||
| �ł́E�E�E�E�Ǝv���Ȃ��璭�߂Ă��܂����B | |||
| �@���l�`�傳�ɒ┑���́u�U�v�́A���̏ꏊ���炾�Ƃقڐ��ʂɌ����܂��B | |||
| �f�b�L�͔��w�ł����A�܂�ő傫�ȃ}���V�����̂悤�ł��ˁB | |||

�V���{���K�[�f��_�P |

�V���{���K�[�f��_�Q |

�V���{���K�[�f��_�R |
|

�V���{���K�[�f��_�S |

�U���ʁ@ |

�u���܁v���ϐg�H |
| �@�@�@�@�@�@�@�@�@�@�@�@�y���l�����z��� | |||
| �@�y���l�����z���ɂ��� |

�`���[���b�v����ϐg |

�x�C�X�^�[�Y�E�g�s�A���[ |
|
| ������Ă݂܂����B | |||
| �@�S����{�́u�`���[���b | |||
| �v�Ղ�v�̉₩���͎p�� | |||
| �����A�u�����̉ԁv������ | |||
| �ł��l�ڂɕt���悤�ɂ� | |||
| �撣���Ă��܂����B | |||
| �@ | |||

����_�P |

����_�Q |

����_�R |
| �@�@�@�@�@�@�@�@�@�@�@�@�@�Ⴈ���Ɂ� | |||
| �@�u���U���Ă��A�Ԑ���I�v�́A���N1��f�ڂ��̂ł� |

����̃o���@ |
||
| �����A���N�͉��l�s�Łu��33�� �S���s�s�Ή��悱�͂� | |||
| �t�F�A�v���R��25������U���S���܂ŊJ�Â���Ă���� | |||
| �W�ŁA�Ԃ̘b�肪�����T��킽���Čf�ڂ���`�ɂȂ�� | |||
| �����B���Ɍ㔼�̂Q��͉��l�s�̉ԁu�o���v�̃I���p�� | |||
| �[�h�ƂȂ��Ă��܂��܂����B | |||
| �@�Ԃ̔������A�f���炵�������͂��ł����ł��傤���H | |||
| �@�䂪�Ƃ̂����₩�Ȓ�ɂ��o���̌Ö���{����A�� | |||
| �N�A�t�E�H�ɔ�r�I�傫�ȉԂ��炩���Ă��܂��B���N�͍�N�H�ə���̂������H���A | |||
| �Q���O�A�l�ƏW�c�ŏo�Ă��Č����ڂɒ���^�̉Ԃ��炩���Ă���悤�Ɍ����܂��B | |||
| �ʐ^�͎l���Q���J�Ԃ������ł��B�o���ɑ���m���̂Ȃ����ɂƂ��ẮA�܂��Ƃ� | |||
| �s�v�c�Ȍ��ہI�Ƃ����������l�s���炵���H�o���̉Ԃ̔������ɍ��ꍞ��ł��鎟�� | |||
| �ł��B | |||
| 2017. 5.23 | ���c | �@���U���Ă��A�Ԑ���I2017�N��: ���̂S |  |
| �@���U���Ă��A�Ԑ���I2017�N��: ���̂S | ���l�s�@�@���c�@�� �@ | |
| �@���U���Ă��A�u�S���s�s�Ή��悱�͂܃t�F�A�v�J�ÂʼnԁI�ԁI�Ԑ���I | |||
| �@�@�@�@�@�@�@�@�@�@�@�@�@��͂��߂Ɂ� | |||
| �@���N�́g���U���Ă��A�Ԑ���h�́A���l�s�Łu�S���s�s�Ή��悱�͂܃t�F�A�v���U | |||
| ���S���܂ŊJ�Â���Ă���܂��̂ŁA�܂������܂��B�S���̃`���[���b�v���S�̉Ԃ� | |||
| ��A�T���ɓ���u�o���v������ƂȂ�܂����B | |||
| �@�u�o���v�̉��Ƃ��ẮA�y���{��ʂ�z���A�y�R�������z���A�y�`�������� | |||
| �u�����z���̎O��ꂪ���ǂ���ł���܂��B | |||
| �@�����?���U���Ă��A�Ԑ���h�̑��҂Ƃ����`�łT��19���Ɏʐ^���B���Ă������� | |||
| ���Q��ɂ킽���Ă��Љ�����܂��B | |||
| �@�@�@�@�@�@�@�@�@�@�@�y���{��ʂ�z��� | |||
| �@�y���{��ʂ�z���́A?�����̏o�W�Ԓd�h�͈������� |

�_�ސ쌧���O�̃t�����[�^���[ |
||
| �Ԃ����ւ��Č��݂ł����A���S�̂́u�o���I�v�Ɋ� | |||
| �S�ɐ�̂���Ă��܂��Ă���܂��B | |||
| �@�_�ސ쌧���O�ɂ́A?���l�O���h�i�L���O�̓��E�E�_ | |||
| �ސ쌧���{���ɁA�N�C���̓��E�E���l�ŊցA�W���b�N�� | |||
| ���E�E���l�s�J�`�L�O�فj�Ɉ��݁A�S���̑��Ԃ���o�� | |||
| �̃t�����[�A�[�g�������܂��B | |||
| �@�u���̂Q�v�ŏЉ�܂������e�Ƃ͈�ς��A�o������ | |||
| �Ȃ��Ă��܂��܂����B | |||
| �@�S���̓`���[���b�v�𒆐S�Ƃ����u�ؗ�Ȃ�t�̋����v����A�o���𒆐S�Ƃ��� | |||
| �u�ؗ�Ȃ�o���̋����v�ɕς��A�܂��u�o������s�s��c�v�Q�������̂̏o�W�� | |||
| �lj�����܂����B | |||
| �@����ؗ�Ȃ�o���̋����� | |||

�o���̋���_�P |

�o���̋���_�Q |

�o���̋���_�R |
|

�o���̋���_�S |

�o���̋���_�T |

�o���̋���_�U |

�o���̋���_�V |

�o���̋����W |

�o���̋���_�X |

�o���̋���_10 |

�o���̋���_11 |

�o���̋���_12 |
| �@���u�o������s�s��c�v�Q�������̂̏o�W | |||
| �@�u�o������s�s��c�v�Ɋւ��āu�ē��v�ɂ��܂� |

�o�W�S�i_�P |
||
| �Ɓw�o������s�s��c�́A��̕��y�Ȃǂ�ʂ��A�Ԃ� | |||
| �ɂ��ӂ�邤�邨���̂���܂��Â���Ɏ����邱�Ƃ� | |||
| �ڕW�Ƃ��āA�o�����L���Z���Ɉ��D����Ă��鎩���̂� | |||
| ��\�������n�������c�̉�c�ł��B����28�N�S��24�� | |||
| �s�����Q�����܂����B�x | |||
| �@�����������܂��ƒn�����l�s���͂��߁u�o�����s�i���j | |||
| �̉ԁv�ɂ��Ă��܂������̂̏W�܂�ł��B�@ | |||
| �@���炫�ōŐ������I�������́A�܂��c�{�~�ł��ꂩ��炭���̂����O���܂����B | |||

�o�W�S�i_�Q |

�k�C���E�〈��s�i�X�J�[���b�g�C���~�U���j |

�R�`���E���R�s�i�ނ��܁j |
|

�Q�n���E�O���s�i�������̋P���j |

�Q�n���E�ʑ����i�}���A�J���X�j |

�_�ސ쌧�E���l�s�i�͂܂݂炢�j |

���쌧�E����s�i�Ȃ��̏����j |

���쌧�E��钬�i�������̋P���j |

�É����E���c�s�i�~�X���܂��j |

���E���s�i���ɉ����j |

�s�E�_�˒��i�n�C�l�X��j |

���m���E�����s�i�ɂ��������j |

���{�E�L���s�i�s�[�X�j�@ |

���{�E�����s�i�A���W�F���j |

���{�E�ݘa�c�s�i���蚒02�j |

���{�E��؎s�i�����h���j |

�������E�������i������̐��j |

���������E�����s�i�v�����Z�X���̂�j |
| �@�@�@�@�@�@�@�@�@�@�y�`�̌�����u�����z��� | |||
| �@���l�F�R��̋u�̈�ԊC���Ɉʒu���܂��u�`�̌�����u�����v�͓W�]�L��̂ق��ɁA | |||
| ����Љ�܂��u����̒�i�����̂���Ԓd���j�v�Ɓu�C���O���b�V�� ���[�Y�̒� | |||
| �i�C�M���X���m�قƗאځj�v������܂��B | |||
| �@���ፁ��̒�� | |||
| �@��100�i��̍���̃o���⍁��̐A�����W�߂��K�[�f���B���[�Y�A�[�`�ł́A�o�� | |||
| �̃t���O�����X�V�����[���~�蒍���A����ɕ�܂�܂��B | |||

����̒�_�P |

����̒�_�Q |

����̒�_�R |
|

����̒�_�S |

����̒�_�T |

����̒�_�U |

����̒�_�V |

����̒�_�W |

����̒�_�X |
| �@����C���O���b�V�� ���[�Y�̒�� | |||
| �@��150�i��A��1,200���̃C���O���b�V�� ���[�Y�𒆐S�ɁA�V���o�[��u���[�� | |||
| �S�Ƃ������Ԃɂ��F�ʂ̃n�[���j�[����뉀�ł��B | |||
������u�����v |

���[�Y�̒�_�P |

���[�Y�̒�_�Q |
|

���[�Y�̒�_�R |

���[�Y�̒�_�S |

���[�Y�̒�_�T |

���[�Y�̒�_�U |

���[�Y�̒�_�V |

���[�Y�̒�_�W |

���[�Y�̒�_�X |

���[�Y�̒�_10 |

���[�Y�̒�_11 |

���[�Y�̒�_12 |

���[�Y�̒�_13 |

���[�Y�̒�_14 |
| 2017. 5.10 | ���� | �^�e�n�`���E�Ȃ̒��u�A�J�{�V�S�}�_���v�����Ȃ́u����O�������v�ɒlj��w�肳��� |  |
| �^�e�n�`���E�Ȃ̒��u�A�J�{�V�S�}�_���v�����Ȃ́@�@�@�@ | |||
| �u����O�������v�ɒlj��w�肳���@�@ | ���l�s�@�@���� �L�� | |
| �P�D�ȑO����ɐ����������Ƃ��Љ� | |||
| �@���̃z�[���y�[�W��2013�N10��27�����Ɂu�䂪�Ƃ̃G�m�L�ɂ��b��́g�A�J�{�V�S | |||
| �}�_���h����v�Ƒ肵�āA���炵��匉��E�H�����ώ@���A�ŏI�I�ɂ͕W�{���쐬 | |||
| �i���F�W�{�̃��x���ɂ�2013�N�W��20������H���ƋL����Ă���j���Ă��̎ʐ^���� | |||
| ����B���̃^�e�n�`���E�Ȃ̒��͖����Ƃ��ē������k�サ�A���l�n��ɐ������� | |||
| ���ƂɂȂ������̂炵�����A�܂�����ɂ͒��̃}�j�A�������������̂��G�Ƃ��ĉ� | |||
| ���ɂł�������G�m�L��H���Ƃ��Đ����ł���悤�ɂȂ����Ƃ������Ă���B | |||
| �Q�D���Ȃ́u����O�������v�w��̃j���[�X | |||
| �@����Q��24���i���j�̒����A���o���V���̗[���Łu�O������14�펔��ȂNj֎~�v�� | |||
| ���o���̂��ƂɁA���Ȃ̐��Ɖ�c��������A��������ĂV������ɐ��߂������� | |||
| �āA�����Ɏw�肳���ƕ��B�M�҂̂悤�Ɏ�������A�W�{�ɂ܂ō�邱�Ƃ�W�{ | |||
| �̌����┄���Ȃǂ͍����؋֎~����邱�ƂɂȂ�B�W�{�������Ă��邱�Ƃ͂ǂ��� | |||
| ���������邱�ƂɂȂ�̂��낤���B���N���䂪�Ƃ̒�̃G�m�L�Ɂu�A�J�{�V�S�} | |||
| �_���v�̗c������̂��A���ꂩ��b���̊Ԓ��ӂ��Ċώ@�������B | |||
| �@�Q�l�܂łɍ���戵���֎~���w�肳���14��ɂ́u�A�J�{�V�S�}�_���v�̑��A�֓� | |||
| ����l���ɂ����Ē蒅�������Ƃ��m�F����Ă�����̐���H���r�炵�A�͂�ɂ� | |||
| �Ă��܂��u�N�r�A�J�c���J�~�L���v��y�b�g�Ƃ��ėA������Ă����́u�I�L�i | |||
| ���}���o�l�N���K�^�v�̌������{�̍ݗ���Ƃ̌�z��Ƃ��āu�}���o�l�N���K�^���v | |||
| ��10��ނ��w�肳���͗l |

����W�{ |

匂̔����k |
|
| �ł���B�M�҂̒m�l�ŃJ�~ | |||
| �L�����V�̏N�W����ɂ� | |||
| ��Ă��鍂�Z�̍Z�������^ | |||
| �C�A���ꂽ�����a�̎R���� | |||
| �����邪�A�������S�� | |||
| �����Ă��̐V���L����ǂ� | |||
| �ꂽ���ƂƎv���Ă���B | |||
| �@�ēx�A�u�A�J�{�V�S�}�_���v�̎���W�{�̎ʐ^��匂̔����k�̎ʐ^�����������Ė{ | |||
| �e����邱�Ƃɂ��悤�B�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�� | |||
| �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@2017�N�Q��28���i�j�@�L | |||